
一块四边形的地(如图33)(EO∥FK,OH∥KG)内有一段曲折的水渠,现在要把这段水渠EOHGKF改成直的.(即两边都是直线)但进水口EF的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠,以节省工时.那么新渠的两条边应当怎么作?写出作法,并加以证明.
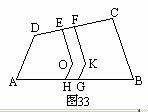
由图34知OK∥AB,延长EO和FK,即得所求新渠.这时,HG=GM(都等于OK),且OK∥AB,故△OHG的面积和△KGM的面积相同.即新渠占地面积与原渠面积相等.而且只挖了△KGM这么大的一块地.
我们再看另一种方法,如图35.
作法:①连结EH,FG.
②过O作EH平行线交AB于N,过K作FG平行线交于AB于M.
③连结EN和FM,则EN,FM就是新渠的两条边界线.
又:EH∥ON
∴△EOH面积=△FNH面积.
从而可知左半部分挖去和填出的地一样多,同理,右半部分挖去和填出的地也![]() 一样多.即新渠面积与原渠的面积相等.
一样多.即新渠面积与原渠的面积相等.
由图35可知,第二种作法用工较多(∵要挖的面积较大).
故应选第一种方法。


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
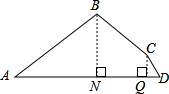 有一块四边形的地ABCD(如图所示),测得AB=26m,BC=10m,CD=5m,顶点B,C到AD的距离分别为10m,4m,则这块地的面积为
有一块四边形的地ABCD(如图所示),测得AB=26m,BC=10m,CD=5m,顶点B,C到AD的距离分别为10m,4m,则这块地的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 一块四边形的地(如图)(EO∥FK,OH∥KG)内有一段曲折的水渠,现在要把这段水渠EOHGKF改成直的.(即两边都是直线)但进水口EF的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠,以节省工时.那么新渠的两条边应当怎么作?写出作法,并加以证明.
一块四边形的地(如图)(EO∥FK,OH∥KG)内有一段曲折的水渠,现在要把这段水渠EOHGKF改成直的.(即两边都是直线)但进水口EF的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠,以节省工时.那么新渠的两条边应当怎么作?写出作法,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
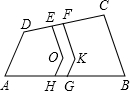 一块四边形的地(如图)(EO∥FK,OH∥KG)内有一段曲折的水渠,现在要把这段水渠EOHGKF改成直的.(即两边都是直线)但进水口EF的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠,以节省工时.那么新渠的两条边应当怎么作?写出作法,并加以证明.
一块四边形的地(如图)(EO∥FK,OH∥KG)内有一段曲折的水渠,现在要把这段水渠EOHGKF改成直的.(即两边都是直线)但进水口EF的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠,以节省工时.那么新渠的两条边应当怎么作?写出作法,并加以证明.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com