
【题目】二次函数y=ax2+2x﹣2,若对满足3<x<4的任意实数x都有y>0成立,则实数a的取值范围为_____.
【答案】a>-![]()
【解析】
方法1:由题意可得ax2+2x-2>0,即为a>![]() 对3<x<4成立,求得右边函数的取值范围,即可得到所求a的范围.
对3<x<4成立,求得右边函数的取值范围,即可得到所求a的范围.
方法二:分情况讨论:①![]() 时,抛物线开口向上,
时,抛物线开口向上,![]() 时符合题意,
时符合题意,![]() 时,由于抛物线对称轴在y轴左侧,可知x=3时y>0,则符合题意;②
时,由于抛物线对称轴在y轴左侧,可知x=3时y>0,则符合题意;②![]() 时,抛物线开口向下,则同时满足x=3,x=4时,y>0,则符合题意.
时,抛物线开口向下,则同时满足x=3,x=4时,y>0,则符合题意.
方法一:解:若对满足3<x<4的任意实数x都有y>0成立,
即有ax2+2x﹣2>0,即为a>![]() ,且 3<x<4,
,且 3<x<4,
由y=![]() 在3<x<4内y随x的增大而增大,
在3<x<4内y随x的增大而增大,
因为当x=3,可得y=![]() =﹣
=﹣![]() ,当x=4,可得y=
,当x=4,可得y=![]() =﹣
=﹣![]() ,
,
所以﹣![]() <
<![]() <﹣
<﹣![]() ,
,
所以a>-![]()
有∵a≠0,
故答案为:a>-![]() 且a≠0.
且a≠0.
方法二:解:①当![]() 时,抛物线开口向上,
时,抛物线开口向上,
若![]() ,则对于任意实数x都有y>0,
,则对于任意实数x都有y>0,
即![]() ,解得
,解得![]() ,
,
与![]() 矛盾,此种情况不存在;
矛盾,此种情况不存在;
若![]() ,即
,即![]() ,解得
,解得![]()
∵抛物线对称轴![]()
∴抛物线在3<x<4时y随x的增大而增大
当x=3时,y>0,则满足3<x<4的任意实数x都有y>0成立
即9a+6-2>0,解得![]()
∴![]() 时,满足3<x<4的任意实数x都有y>0成立
时,满足3<x<4的任意实数x都有y>0成立
②当![]() 时,抛物线开口向下
时,抛物线开口向下
同时满足x=3,x=4时,y>0,则满足3<x<4的任意实数x都有y>0成立
即![]()
解得![]()
∴![]()
故答案为:![]() 或
或![]()


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
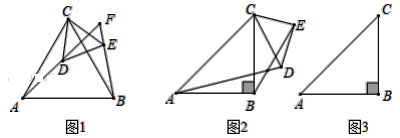
①求证:AD=BE;
②求∠AFB的度数.
(2)如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F.
①求证:AD=![]() BE;
BE;
②若AB=BC=3,DE=EC=![]() .将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
.将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
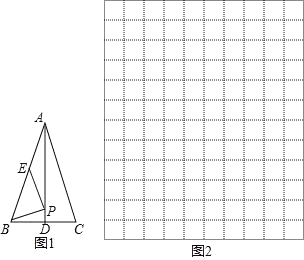
【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 为矩形,连接
为矩形,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(2)如图②,延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图③,将线段![]() 绕点
绕点![]() 旋转一定的角度
旋转一定的角度![]() (
(![]() )得到线段
)得到线段![]() ,连接
,连接![]() ,点
,点![]() 始终为
始终为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.

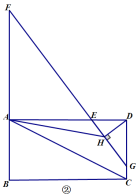

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+4与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,且点B的坐标为(4,0),点E(m,0)为x轴上的一个动点,过点E作直线l⊥x轴,与抛物线y=ax2﹣
x+4与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,且点B的坐标为(4,0),点E(m,0)为x轴上的一个动点,过点E作直线l⊥x轴,与抛物线y=ax2﹣![]() x+4交于点F,与直线AC交于点G.
x+4交于点F,与直线AC交于点G.
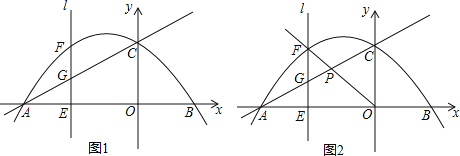
(1)分别求抛物线y=ax2﹣![]() x+4和直线AC的函数表达式;
x+4和直线AC的函数表达式;
(2)当﹣8<m<0时,求出使线段FG的长度为最大值时m的值;
(3)如图2,作射线OF与直线AC交于点P,请求出使FP:PO=1:2时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
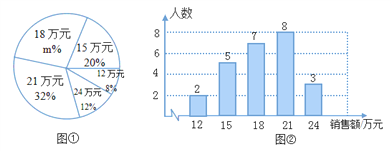
【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com