
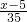 =
=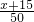 +2
+2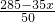 辆50座的,其中x≥0
辆50座的,其中x≥0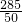 =5.7≈6辆,需要租金:6×300=1800元;
=5.7≈6辆,需要租金:6×300=1800元;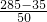 =5,需要租金:250+300×5=1750元;
=5,需要租金:250+300×5=1750元; =4.3≈5辆,需租金:250×2+300×5=2000元;
=4.3≈5辆,需租金:250×2+300×5=2000元;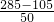 =3.6≈4辆,需租金:3×250+4×300=1950元;
=3.6≈4辆,需租金:3×250+4×300=1950元; =2.9≈3辆,需租金:4×250+3×300=1900元;
=2.9≈3辆,需租金:4×250+3×300=1900元;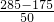 =2.2≈3辆,需租金:5×250+3×300=2150元;
=2.2≈3辆,需租金:5×250+3×300=2150元; =1.5≈2辆,需租金:6×250+2×300=2100元;
=1.5≈2辆,需租金:6×250+2×300=2100元;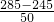 =0.8≈1辆,需租金:7×250+300=2050元;
=0.8≈1辆,需租金:7×250+300=2050元;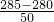 ≈1辆,需租金:8×250+300=2300元;
≈1辆,需租金:8×250+300=2300元;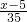 辆,全部换乘50座的需
辆,全部换乘50座的需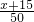 辆,已知:如果全部换乘50座的,则可比35座车少用2辆,以此为等量关系列出方程求解;
辆,已知:如果全部换乘50座的,则可比35座车少用2辆,以此为等量关系列出方程求解;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 行驶的路程(千米) | 速度(千米/时) | 所需时间(小时) | |
| 自行车 | 20 | x | |
| 汽车 | 20 |
查看答案和解析>>
科目:初中数学 来源:云南省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:安徽省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com