
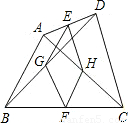
 CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件. AB,同理HF
AB,同理HF AB,∴EG
AB,∴EG HF.
HF. AB,又可同理证得EH=
AB,又可同理证得EH= CD,
CD,

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟试卷冀教版(解析版) 题型:解答题
 ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
查看答案和解析>>
科目:初中数学 来源:2009年浙江省温州市永嘉县二模试卷(解析版) 题型:解答题
 ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
查看答案和解析>>
科目:初中数学 来源:2007年江苏省泰州市中考数学试卷(解析版) 题型:解答题
 ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
查看答案和解析>>
科目:初中数学 来源:2007年江苏省泰州市中考数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com