
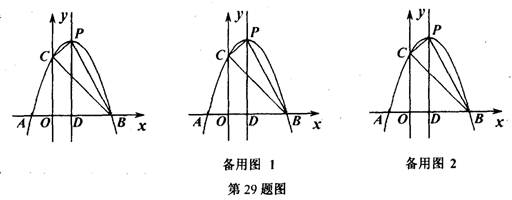
如图,抛物线y=ax2+bx+c的顶点为P,对称轴直线x=1与x轴交于点D,抛物线与x轴交于A、B两点,与y轴交于点C,其中A(-1,0)、C(0,3).
1.求此抛物线的解析式
2.点E在线段BC上,若△DEB为等腰三角形,求点E的坐标
3.点F、Q都在该抛物线上,若点C与点F关于直线x=1成轴对称,连结BF、BQ,如果∠FBQ=45°,求点Q的坐标;
4.将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转后的图形为△BO'C',BO'与BP重合时,则△BO'C'不在BP上的顶点C'的坐标为 ▲ (直接写出答案).
科目:初中数学 来源:2008年江西省南昌市初中毕业升学统一考试、数学试卷 题型:044
如图,抛物线y1=-ax2-ax+1经过点P![]() ,且与抛物线y2=ax2-ax-1,相交于A,B两点.
,且与抛物线y2=ax2-ax-1,相交于A,B两点.

(1)求a值;
(2)设y1=-ax2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤≤x≤xB,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值?其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.

1.⑴求a的值和该抛物线顶点P的坐标.
2.⑵求DPAB的面积;
3.⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.
【小题1】⑴求a的值和该抛物线顶点P的坐标.
【小题2】⑵求DPAB的面积;
【小题3】⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.

1.⑴求a的值和该抛物线顶点P的坐标.
2.⑵求DPAB的面积;
3.⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com