
【题目】如图,正方形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,折叠正方形纸片,使
,折叠正方形纸片,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后折痕
重合,展开后折痕![]() 分别交
分别交![]() 于点
于点![]() ,连
,连![]() 给出下列结论,其中正确的个数有( )
给出下列结论,其中正确的个数有( )
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .
.
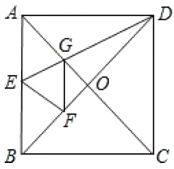
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①由ABCD是正方形,可得到三角形ACD是等腰直角三角形,则可以得到![]() 的度数;
的度数;
②证![]() ,得AG=FG,由FG>OG即可得;
,得AG=FG,由FG>OG即可得;
③证四边形![]() 四边的关系,再判断是否是菱形;
四边的关系,再判断是否是菱形;
④设OA=a,证![]() ,得
,得![]() ,易得
,易得![]() ,类似可得
,类似可得![]() ,即可得到OF与BF的关系.
,即可得到OF与BF的关系.
解:①∵ABCD是正方形
∴三角形ACD是等腰直角三角形
因此![]()
故①错误;
② 由折叠性质可得:AE=EF, ![]() ,
,
在![]() 和
和![]() 中,
中,
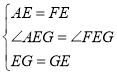
∴![]() (SAS)
(SAS)
∴AG=FG
∵在直角三角形GOF中,AG=FG>GO,
∴![]()
故②错误;
③ ∵![]() ,
,
![]() ,
,
∴![]()
∴ AE=AG,
又∵AE=FE,AG=FG,
∴AE=EF=GF=AG,
∴四边形![]() 是菱形
是菱形
故③正确;
④ 设OF=a
∵由②的解析过程知道![]()
∴![]() ,
,
又∵![]() ,
,
∴![]()
∵在直角三角形OFG中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵在直角三角形EBF中,![]() ,
,
即![]() ,
,
故④正确;
综上,只有③④两个正确,故选B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过B(3,0),C(0,-3)两点,点D为顶点.
经过B(3,0),C(0,-3)两点,点D为顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)点E在抛物线的对称轴上,F在BD上,求BE+EF的最小值;
(3)点P是抛物线第四象限的点(不与B、C重合),连接PB,以PB为边作正方形BPMN,当点M或N恰好落在对称轴上时,求出对应的P点的坐标(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
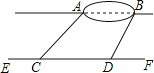
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
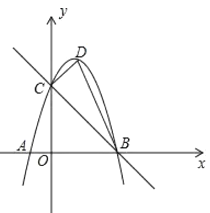
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() .
.
(1)求抛物线的表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上有一点
上有一点![]() ,若使
,若使![]() 的值最小,则点
的值最小,则点![]() 的坐标为____________.
的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
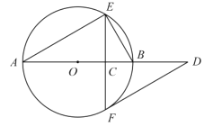
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
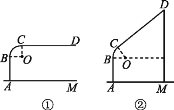
【题目】如图是一个桌面会议话筒示意图,中间BC部分是一段可弯曲的软管,在弯曲时可形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,已知AB的长10 cm,CD的长为25.2 cm.
(1)如图①,若话筒弯曲后CD与桌面AM平行,此时CD距离桌面14 cm,求弧BC的长度(结果保留π);
(2)如图②,若话筒弯曲后弧BC所对的圆心角度数为60°,求话筒顶端D到桌面AM的距离(结果保留一位小数).(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com