
 的最小值;
的最小值; 的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m,n ,k的取值是否有关?请说明理由。
的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m,n ,k的取值是否有关?请说明理由。
解:(1)据题意,∵a+h= , ,∴所求正方形与矩形的面积之比:  , ,∵  ∴  由  知m,k同号, 知m,k同号, ∴mk>0 ∴  即正方形与矩形的面积之比不小于4; |
|
| (2)∵∠FED=90°, ∴DF为⊙O的直径, ∴⊙O的面积为:  , ,矩形PDEF的面积:  , ,∴面积之比:  , ,设   , , , ,∵  ∴  ∴  即  时(EF=DE), 时(EF=DE), 的最小值为 的最小值为 ; ; |
|
(3)当 的值最小时,这时矩形PDEF的四边相等为正方形, 的值最小时,这时矩形PDEF的四边相等为正方形,过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP=e, ∵BN∥FE,NF∥BE, ∴BN=EF, ∴BN =FP=e, 由BC∥MQ,得:BM=AG=h, ∵AQ∥BC,PF∥BC, ∴AQ∥FP, ∴△FBP∽△ABQ, ∴  , ,∴  , ,∴  , ,∴  ∴线段AQ的长与m,n,k的取值有关。 |
 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
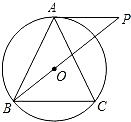 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
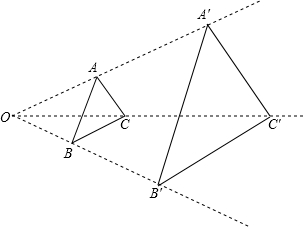
| OA′ |
| OA |
| OB′ |
| OB |
| OC′ |
| OC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com