解:(1)∵AB的⊙O的直径,
∴∠C=∠D=90°,
∵D是上半圆中点,
∴AD=BD,
∴△ABD是等腰直角三角形,
在Rt△ABC中,AB=

=

,
∴AD=

AB=


,
∴四边形ACBD的面积S=S
△ABC+S
△ABD,
=

AC•BC+

AD
2,
=

mn+

×

(m
2+n
2),
=

(m+n)
2;
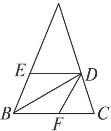
(2)如图①,过点D作DM⊥AC于M,作DN⊥BC交CB的延长线于N,则四边形DMCN是矩形,
∴∠BDN+∠BDM=90°,

又∵∠ADM+∠BDN=∠ADB=90°,
∴∠ADM=∠BDN,
∵在△ADM和△BDN中,
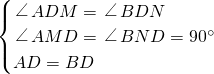
,
∴△ADM≌△BDN(AAS),
∴AM=BN,DM=DN,
∴矩形DMCN是正方形,
设正方形的边长为x,AM=BN=y,则

,
解得

,
tan∠DAC=
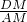
=

=
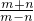
;
(3)结论不成立,点C在

上时,tan∠DAC=

;
点C在

上时,tan∠DAC=

.
理由如下:点C在

上时,
如图②,点C′为点C关于原点的对称点,连接AC′、BC′,
则四边形AC′C是矩形,
∴AC′=BC=n,BC′=AC=m,
过点D作DM⊥AC′于M,作DN⊥BC′交C′B的延长线于N,
与(2)同理可求,AM=BN,DM=DN,
∴矩形DMCN是正方形,
设正方形的边长为x,AM=BN=y,则
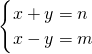
,
解得

,
∵DM⊥AC′,AC′∥BC,
∴DM⊥BC,
∵∠C=90°,
∴AC∥DM,
∴∠DAC=∠ADM,
∴tan∠DAC=tan∠ADM=

=

=

;
点C在

上时,如图③,
设正方形的边长为x,AN=BM=y,则

,
解得

,
tan∠DAC=tan∠ADN=
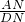
=

=

.
分析:(1)根据直径所对的圆周角是直角可得∠C=∠D=90°,根据等弧所对的弦相等可得AD=BD,从而得到△ABD是等腰直角三角形,利用勾股定理列式求出AB,再根据等腰直角三角形的性质求出AD,然后根据四边形ACBD的面积S=S
△ABC+S
△ABD,列式计算即可得解;
(2)过点D作DM⊥AC于M,作DN⊥BC交CB的延长线于N,可得四边形DMCN是矩形,根据同角的余角相等求出∠ADM=∠BDN,然后利用“角角边”证明△ADM和△BDN全等,根据全等三角形对应边相等可得AM=BN,DM=DN,从而得到矩形DMCN是正方形,设正方形的边长为x,AM=BN=y,然后用m、n表示a列出方程组求解得到x、y,再根据锐角的正切值等于对边比邻边列式计算即可得解;
(3)图②,先求出点C关于原点的对称点C′,连接AC′、BC′,根据对角线互相平分且相等的四边形是矩形可得四边形AC′C是矩形,过点D作DM⊥AC′于M,作DN⊥BC′交C′B的延长线于N,然后与(2)的思路相同求解即可;图③同理可求.
点评:本题考查了圆的综合题型,主要利用了直径所对的圆周角是直角,等腰直角三角形的判定与性质,全等三角形的判定与性质,锐角的正切的定义,作辅助线构造出全等三角形与正方形是解题的关键,也是本题的难点.

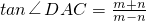 ;
; 或
或 上时,②中结论是否成立?若成立,请说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案,并选择其中一种证明)
上时,②中结论是否成立?若成立,请说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案,并选择其中一种证明)
 =
= ,
, AB=
AB=
 ,
, AC•BC+
AC•BC+ AD2,
AD2, mn+
mn+ ×
× (m2+n2),
(m2+n2), (m+n)2;
(m+n)2;
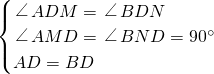 ,
, ,
, ,
,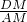 =
= =
=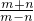 ;
; 上时,tan∠DAC=
上时,tan∠DAC= ;
; 上时,tan∠DAC=
上时,tan∠DAC= .
. 上时,
上时,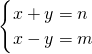 ,
, ,
, =
= =
= ;
; 上时,如图③,
上时,如图③, ,
, ,
,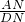 =
= =
= .
.

 ,以BC为直径作半圆BFC,则商标图案面积等于________cm2.
,以BC为直径作半圆BFC,则商标图案面积等于________cm2.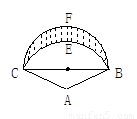
![]() 个等腰三角形.
个等腰三角形.