
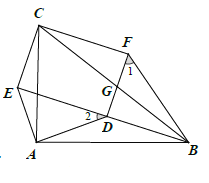
【题目】如图1,![]() 是
是![]() 内任意一点,连接
内任意一点,连接![]() ,分别以
,分别以![]() 为边作
为边作![]() (
(![]() 在
在![]() 的左侧)和
的左侧)和![]() (
(![]() 在
在![]() 的右侧),使得
的右侧),使得![]() ,
,![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)如图2,![]() 交于点
交于点![]() ,若
,若![]() ,点
,点![]() 共线,其他条件不变,
共线,其他条件不变,
①判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②当![]() ,
,![]() ,且四边形
,且四边形![]() 是正方形时,直接写出
是正方形时,直接写出![]() 的长.
的长.

【答案】(1)证明见解析;(2)①四边形![]() 是矩形.理由见解析;②
是矩形.理由见解析;②![]() .
.
【解析】
(1)根据![]() ,得到
,得到![]() ,
,![]() ,再证
,再证![]() ,
,![]()
方法一:通过证明![]() ,
,![]() ,从而四边形
,从而四边形![]() 是平行四边形,
是平行四边形, ![]() ,所以为矩形.
,所以为矩形.
方法二:证明![]()
方法三:证![]() ,
,![]() ,
,![]() .
.
(1)∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,即.
,即.![]() .
.
∴![]() .
.
(2)①四边形![]() 是矩形.理由如下:
是矩形.理由如下:
方法一:由(1)知,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,即
,即![]() .
.
∴![]() . ∴
. ∴![]() .
.
∵![]() . ∴
. ∴![]() .
.
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
方法二:如图
由(1)知![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,
,![]() ,即
,即![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,
共线,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是矩形.
是矩形.
方法三:由(1)知,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(1)知![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,点
,点![]() 共线,∴
共线,∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() . ∵
. ∵![]() ,∴
,∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
②![]()


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
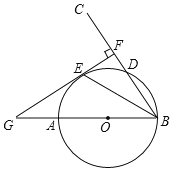
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() =
=![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
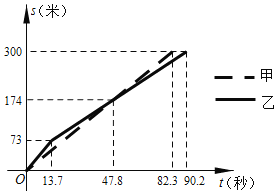
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A. 乙队率先到达终点
B. 甲队比乙队多走了![]() 米
米
C. 在![]() 秒时,两队所走路程相等
秒时,两队所走路程相等
D. 从出发到![]() 秒的时间段内,乙队的速度慢
秒的时间段内,乙队的速度慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
(1)请你画出它的从正面看和从左面看的形状图.
(2)如果每个立方体的棱长为2cm,则该几何体的表面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 三点
三点
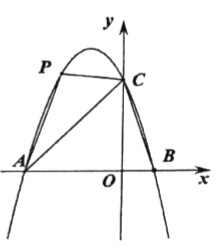
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半?若存在,求出点
的面积的一半?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)点![]() 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出点
为顶点的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 在斜边
在斜边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径作圆,分别与
为半径作圆,分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
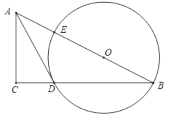
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求劣弧
,求劣弧![]() 与弦
与弦![]() 所围阴影图形的面积;
所围阴影图形的面积;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
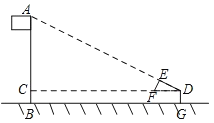
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com