
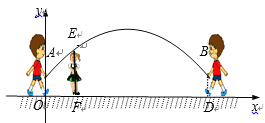
【题目】跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为![]() .
.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围_______________.
【答案】(1)![]() ;(2)绳子不能顺利从他头顶越过;(3)1<t<5.
;(2)绳子不能顺利从他头顶越过;(3)1<t<5.
【解析】
(1)选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入求出解析式即可;
(2)将函数解析式配方成顶点式,得到函数的最大值,据此即可作出判断;
(3)实质上就是求y=1.4时,对应的x的两个值,就是t的取值范围.
解:(1)由题意得点E(1,1.4),B(6,0.9),代入![]() 得
得
![]() ,解得:
,解得: ![]() ,
,
∴所求的抛物线的解析式是![]() ;
;
(2)∵![]() ,
,
∵![]() ,
,
∴x=3时,y有最大值为1.8,
∵1.85>1.8,
∴绳子不能顺利从他头顶越过;
(3)身高在1. 4米到1. 7米之间的人站在OD之间,
∵1.4<1.7<1.8,
∴只需要计算1.4米身高的情况.
当y=1.4时,![]() ,
,
解得![]() ,
,
∴1<t<5,故答案为:1<t<5.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
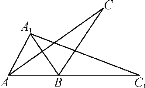
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
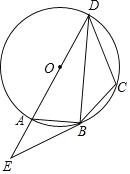
(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
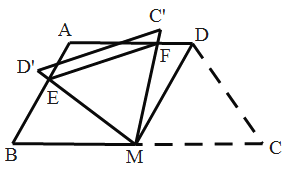
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (
(![]() )同时与
)同时与![]() 交于一点
交于一点![]() 时,点
时,点![]() ,
,![]() 和点
和点![]() 构成
构成![]() ,在此过程中,
,在此过程中,![]() 周长的最小值是__________.
周长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
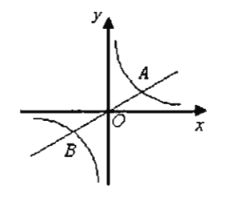
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (
(![]() )交于
)交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为6.
的横坐标为6.
(1)求![]() 的值;
的值;
(2)若双曲线![]() (
(![]() )上一点
)上一点![]() 的纵坐标为9,求
的纵坐标为9,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() (
(![]() )于
)于![]() ,
,![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点组成的四边形面积为96,求点
为顶点组成的四边形面积为96,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
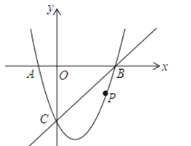
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点,过点P作平行于y轴的直线PM,交线段BC于M,当△PCM是以PM为腰的等腰三角形时,点P的坐标是( )
A.(2,-3)或(![]() +1,—2)B.(2,-3)或(
+1,—2)B.(2,-3)或(![]() ,-1-2
,-1-2![]() )
)
C.(2,-3)或(![]() ,-1-2
,-1-2![]() )D.(2,-3)或(3-
)D.(2,-3)或(3-![]() ,2-4
,2-4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
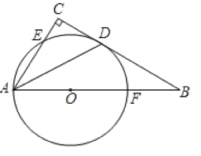
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com