
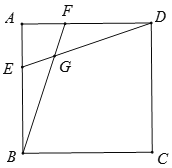
【题目】如图,在正方形ABCD中,AB=a,E、F分别是AB、AD边上的点,BF,DE相交于点G,若AE=![]() AB,AF=
AB,AF=![]() AD,则四边形BCDG的面积是( )
AD,则四边形BCDG的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如图,以点B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,建立平面直角坐标系,连接CG,过点G作GM⊥BC,GN⊥DC,分别求得直线BF和直线DE的解析式,从而可求得点G的坐标,则利用S四边形BCDG=S△BCG+S△DCG,可求得答案.
如图,以点B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,建立平面直角坐标系,连接CG,过点G作GM⊥BC,GN⊥DC

∵在正方形ABCD中,AB=a,AE=![]() AB,AF=
AB,AF=![]() AD,
AD,
∴点B(0,0),E(0,![]() ),F(
),F(![]() ,a),D(a,a),
,a),D(a,a),
∴直线BF的解析式为:y=3x,
设直线DE的解析式为:y=kx+b,
将E(0,![]() ),D(a,a)代入得:
),D(a,a)代入得: ,
,
解得: ,
,
∴直线DE的解析式为y=![]() x+
x+![]() ,
,
由 ,
,
得: ,
,
∴G(![]() ,
,![]() ),
),
∴S四边形BCDG=S△BCG+S△DCG
=![]() BCGM+
BCGM+![]() CDGN
CDGN
=![]() (GM+GN)×a
(GM+GN)×a
∵GM=yG=![]() ,GN=a﹣
,GN=a﹣![]() =
=![]() ,
,
∴S四边形BCDG=![]() ×(
×(![]() +
+![]() )×a=
)×a=![]() .
.
故选:C.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
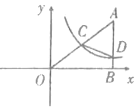
【题目】如图,在平面直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象的一支经过
的图象的一支经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() .
.
(1)求该反比例函数的表达式;
(2)若函数![]() 与
与![]() 的图象的另一支交于点
的图象的另一支交于点![]() ,求三角形
,求三角形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的![]() ,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
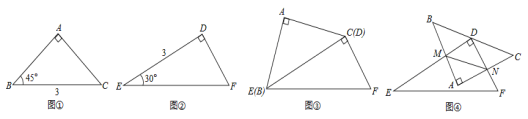
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量某特种车辆的性能,研究制定了行驶指数![]() ,而
,而![]() 的大小与平均速度
的大小与平均速度![]() 和行驶路程
和行驶路程![]() 有关(不考虑其他因素),
有关(不考虑其他因素),![]() 由两部分的和组成,一部分与
由两部分的和组成,一部分与![]() 成正比,另一部分与
成正比,另一部分与![]() 成正比.在实验中得到了表格中的数据:
成正比.在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
(1)用含![]() 和
和![]() 的式子表示
的式子表示![]() ;
;
(2)当行驶指数为![]() ,而行驶路程为
,而行驶路程为![]() 时,求平均速度的值;
时,求平均速度的值;
(3)当行驶路程为![]() 时,若行驶指数值最大,求平均速度的值.
时,若行驶指数值最大,求平均速度的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
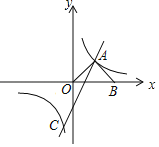
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,我市享有“江南八达岭”美誉的江南长城旅游区,为吸引游客组团来此旅游,特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格60元/人;
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于50元/人.
(1)若某单位组织23名员工去江南长城旅游区旅游,购买门票共需费用多少元?
(2)若某单位共支付江南长城旅游区门票费用共计1232元,试求该单位这次共有多少名员工去江南长城旅游区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
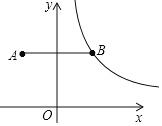
【题目】在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=![]() (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(1)求k的值;
(2)若△ABP的面积等于2,求点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com