练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，已知抛物线与直线都经过，两点，该抛物线的顶点为．

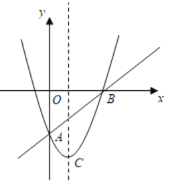
    （1）求抛物线和直线的解析式;

    （2）设点是直线下方抛物线上的一动点，求面积的最大值，并求面积最大时，点的坐标．

    【答案】（1）抛物线解析式：;直线的解析式：;（2）面积的最大值是,此时点坐标为．

    【解析】

    （1）将A（0，-3）、B（3，0）两点坐标分别代入二次函数的解析式和一次函数解析式即可求解;

    （2）作PG∥y轴交直线AB于点G，设P（m，m2-2m-3），则G（m，m-3），可由S△PAB＝PGOB，得到m的表达式，利用二次函数求最值问题配方即可．

    解：（1）抛物线经过，两点，

    抛物线的解析式为

    直线经过，两点

    解得

    直线的解析式为

    （2）如图，作轴交直线于点，交轴于．

    设，则

    ．

    当时，面积的最大值是，此时点坐标为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

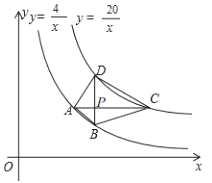
    【题目】如图，四边形ABCD的四个顶点分别在反比例函数与的图象上，对角线轴，且于点P．已知点B的横坐标为4．

    （1）若点P的纵坐标为2，求直线AB的函数表达式．

    （2）若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作，交射线OB于点D，连接CD；

    （2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；

    （3）连接OM，MN．

    根据以上作图过程及所作图形，下列结论中错误的是（ ）

    A. ∠COM=∠CODB. 若OM=MN，则∠AOB=20°

    C. MN∥CDD. MN=3CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

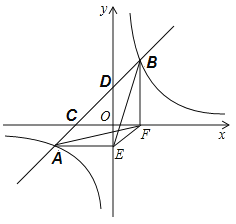
    【题目】在一次数学课上，李老师出示一道开放题，让同学们依据已知条件写出正确结论，具体如下：如图，直线与双曲线相交于，两点，过点和分别作轴和轴的垂线，垂足分别为，，连接，，，直线与轴和轴分别交于点，．若点坐标，请写出正确结论．聪明的强强很快写出了四个结论，其中不正确的结论是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.掷一枚均匀的骰子，骰子停止转动后，点朝上是必然事件

    B.了解一批灯泡的使用寿命，适合用普查的方式．

    C.从五张分别写着，，，，的卡片中随机抽取张，是无理数的概率是．

    D.甲乙两人在相同条件下各射击次，他们的成绩平均数相同，方差分别是，，则甲的射击成绩较稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在函数学习中，我们经历了“确定函数表达式一利用函数图象研究其性质一运用函数解决问题”的学习过程，在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象，同时我们也学习了绝对值的意义|a|，结合上面经历的学习过程，现在来解决下面的问题：在函数y＝|kx﹣1|+b，当x＝1时，y＝﹣2；当x＝0时，y＝﹣1．

    （1）求这个函数的表达式；

    （2）请你结合以下表格在坐标系中画出该函数的图象．

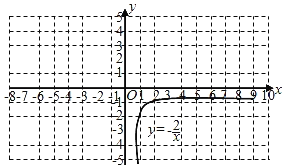
    （3）观察这个函效图象，请写出该函数的两条性质；

    （4）已知函数y＝﹣（x＞0）的图象如图所示，请结合图象写出|kx﹣1|﹣﹣b（x0）的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，OC长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

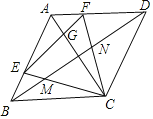
    【题目】如图，已知边长为4的菱形ABCD中，AC＝BC，E，F分别为AB，AD边上的动点，满足BE＝AF，连接EF交AC于点G，CE、CF分别交BD与点M，N，给出下列结论：①∠AFC＝∠AGE；②EF＝BE+DF；③△ECF面积的最小值为3，④若AF＝2，则BM＝MN＝DN；⑤若AF＝1，则EF＝3FG；其中所有正确结论的序号是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y=kx+b（k≠0）的图象经过点A（2，-6），且与反比例函数y=-的图象交于点B（a，4）

    （1）求一次函数的解析式；

    （2）将直线AB向上平移10个单位后得到直线l：y1=k1x+b1（k1≠0），l与反比例函数y2= 的图象相交，求使y1＜y2成立的x的取值范围．

    查看答案和解析>>

    同步练习册答案