如图,在△ABC中,∠ACB=Rt∠,AC=3,AB=5,过点A作AD⊥AB交BC的延长线于点D.动点P从点B出发以每秒3个单位的速度沿B-A-D方向向终点D运动,另一动点Q从点A出发以每秒2个单位的速度沿A-C-B方向向终点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终点,则另一点也立即停止运动.设动点运动的时间为t秒.
(1)求线段AD的长;
(2)当点Q在线段AC上时,求△APQ的面积S关于t的函数关系式并写出自变量t的取值范围;
(3)请探索:在整个运动过程中,是否存在某一时刻t,使得直线PQ与△ABC的一边平行?若存在,请求出所有满足条件t的值;若不存在,请说明理由;
(4)当t=______
【答案】
分析:(1)根据勾股定理求得BC=4;然后利用相似三角形△ADC∽△BAC的对应边成比例知

=
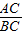
,由此可以求得线段的长度;
(2)作辅助线PM(过点P作PM⊥AC于点M)构建平行线PM∥BC,然后利用平行线截线段成比例知
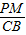
=
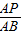
,即PM=

(5-3t),最后由三角形的面积公式即可列出△APQ的面积S关于t的函数关系式;
(3)需要分类讨论:当PQ∥BC、PQ∥AC以及PQ∥AB时,由平行线截线段成比例列出比例式,即可求得相应的t值;
(4)①当点P与点D重合、点Q在线段BC上时,点P、Q、D恰好在同一条直线上;②如图5,当点P在线段AB上,点Q在线段AC上时,点P、Q、D恰好在同一条直线上.
解答: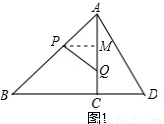
解:(1)∵∠ACB=90°,AC=3,AB=5,
∴BC=4(勾股定理);
又∵AD⊥AB,
∴∠BAD=90°.
∵∠D+∠CAD=90°,∠CAD+∠BAC=90°,
∴∠D=∠BAC(等量代换),
又∵∠ACD=∠BCA=90°,
∴△ADC∽△BAC,
∴
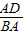
=
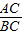
(相似三角形的对应边成比例),即
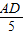
=

,
∴AD=
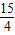
;
(2)如图1,过点P作PM⊥AC于点M.
∵∠ACB=90°,
∴BC⊥AC,
∴PM∥BC,
∴
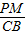
=
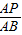
(平行线截线段成比例).
∵BC=4,AP=5-3t,AB=5,
∴PM=

(5-3t),
∴S=

AQ•PM=

×2t×

(5-3t)=-
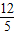
t
2+4t(0≤t≤

);
(3)存在,有三种情况:
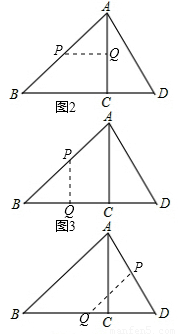
如图2,当0≤t≤

时,令PQ∥BC,得
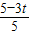
=
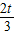
,解得t=
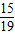
;
如图3,当

<t≤

时,令PQ∥AC,得
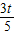
=
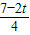
,解得t=
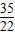
;
如图4,当

<t<
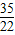
时,令PQ∥AB,得
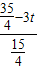
=
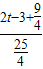
,解得,t=
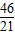
;
综上所述,当t=
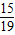
或
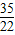
或
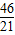
时,直线PQ与△ABC的一边平行.
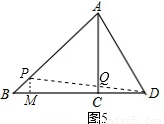
(4)当点P与点D重合、点Q在线段BC上时,点P、Q、D恰好在同一条直线上,
此时t=
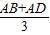
=
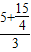
=
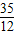
.
如图5,当点P在线段AB上,点Q在线段AC上时,点P、Q、D恰好在同一条直线上.
过点P作PM⊥BC于点M.则QC∥PM.
∵sin∠B=
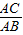
=
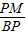
,即

=
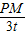
,解得PM=
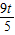
;
cos∠B=
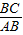
=
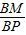
,即

=
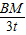
,解得BM=
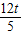
.
∵△ADC∽△BAC,
∴
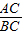
=
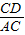
,即

=
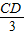
,解得CD=

,
∴DM=CD+BC-BM=
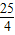
-
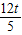
.
∵QC∥PM,
∴
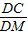
=
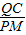
(平行线分线段成比例),即
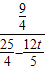
=
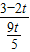
,解得t=
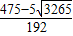
.
则t=
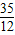
或
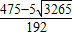
.
故答案是:
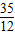
或
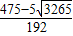
.
点评:本题考查了相似综合题:相似三角形的判定与性质、勾股定理、平行线截线段成比例等知识点的综合运用.

 =
=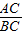 ,由此可以求得线段的长度;
,由此可以求得线段的长度;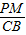 =
=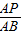 ,即PM=
,即PM= (5-3t),最后由三角形的面积公式即可列出△APQ的面积S关于t的函数关系式;
(5-3t),最后由三角形的面积公式即可列出△APQ的面积S关于t的函数关系式; 解:(1)∵∠ACB=90°,AC=3,AB=5,
解:(1)∵∠ACB=90°,AC=3,AB=5,
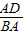 =
=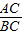 (相似三角形的对应边成比例),即
(相似三角形的对应边成比例),即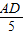 =
= ,
,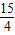 ;
;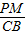 =
=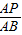 (平行线截线段成比例).
(平行线截线段成比例). (5-3t),
(5-3t), AQ•PM=
AQ•PM= ×2t×
×2t× (5-3t)=-
(5-3t)=-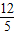 t2+4t(0≤t≤
t2+4t(0≤t≤ );
); 时,令PQ∥BC,得
时,令PQ∥BC,得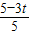 =
=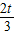 ,解得t=
,解得t=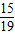 ;
; <t≤
<t≤ 时,令PQ∥AC,得
时,令PQ∥AC,得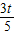 =
=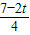 ,解得t=
,解得t=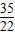 ;
; <t<
<t<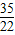 时,令PQ∥AB,得
时,令PQ∥AB,得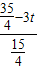 =
=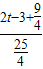 ,解得,t=
,解得,t=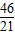 ;
;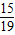 或
或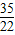 或
或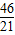 时,直线PQ与△ABC的一边平行.
时,直线PQ与△ABC的一边平行.
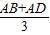 =
=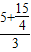 =
=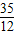 .
.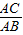 =
=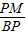 ,即
,即 =
=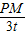 ,解得PM=
,解得PM=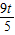 ;
;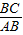 =
=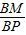 ,即
,即 =
=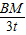 ,解得BM=
,解得BM=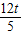 .
.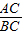 =
=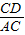 ,即
,即 =
=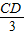 ,解得CD=
,解得CD= ,
,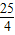 -
-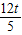 .
.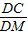 =
=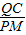 (平行线分线段成比例),即
(平行线分线段成比例),即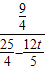 =
=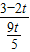 ,解得t=
,解得t=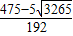 .
.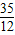 或
或 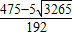 .
.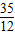 或
或 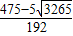 .
.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为