
����Ŀ������������8�֣�����ʵ����ѧ����ҵ��������������ҵ�ĸ��һ����Ҫ�ٴ룮ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ�����ҵʱ�䣬�����ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ���A��1Сʱ���ڣ�B��1Сʱ-1��5Сʱ��C��1��5Сʱ-2Сʱ��D��Сʱ���ϣ����ݵ�������������ͼ��ʾ��������������ͳ��ͼ�������ͼ����Ϣ����������⣺
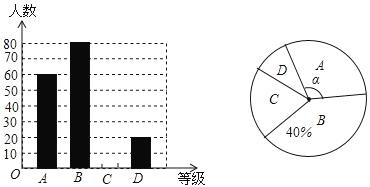
��1����У��������_________��ѧ����
��2���뽫����ͳ��ͼ����������
��3����ʾ�ȼ�A������Բ�Ľ�![]() �Ķ�����____________��
�Ķ�����____________��
��4���ڴ˴��ʾ������У��ס����������2��ƽ��ÿ�������ҵʱ�䶼��2Сʱ���ϣ�����4������ѡ2��ȥ�μ���̸�����б�����״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
���𰸡���1��200�ˣ���2������������3��![]() ����4��
����4��![]() ��
��
��������
���⣨1��������ͼ�����ǿ��Կ��ó�A������Ϊ60��B������Ϊ80��D������Ϊ20��������ͳ��ͼ�������ܿ���Bռ�ı���40%���������Ǻ������ܵó���������200�ˣ�
��2���������ܵó�C������40�ˣ�ͼ�ο������в��䣩��
��3��Aռ�ı��ؼ�����Բ�Ľ�![]() �Ķ���Ϊ��
�Ķ���Ϊ��![]() =
=![]() ��
��
���������ѧ�����Ƿֱ��ʾΪ��A����B����A����B����һ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������Ǿͺ����ó��������Բ�ͬ�༶�ĸ���Ϊ��
���������Ǿͺ����ó��������Բ�ͬ�༶�ĸ���Ϊ��![]()
�����������1���⣺��1��200����2����ͼ���£�

��2���⣺60��200=30%��
��3���⣺��װ�ѧ��Ϊ![]() ��
��![]() �������п��ܵ����Ϊ��
�������п��ܵ����Ϊ��![]() ������
������![]() ����
����
��![]() ����
����![]() ����
����![]() ��
��![]() ������������Բ���ͬһ�����������֣�����Ϊ
������������Բ���ͬһ�����������֣�����Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬
�㣬![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() .
.
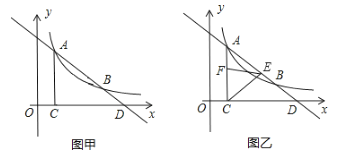
��1����ͼ�ף����������Ľ���ʽ��![]() ������ꣻ
������ꣻ
��2����ͼ�ң�����![]() ���߶�
���߶�![]() ���˶�������
���˶�������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��.��˵��
��.��˵��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y����![]() x2+bx+c��ֱ��y��
x2+bx+c��ֱ��y��![]() x��3�ֱ�x�ᡢy���ϵ�B��C���㣬�����������x�����һ������Ϊ��A������Ϊ��D������CD��x���ڵ�E��
x��3�ֱ�x�ᡢy���ϵ�B��C���㣬�����������x�����һ������Ϊ��A������Ϊ��D������CD��x���ڵ�E��
��1����������ߵı���ʽ����D�����ꣻ
��2�����DCB������ֵ��
��3�������F��y���ϣ��ҡ�FBC����DBA+��DCB�����F�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
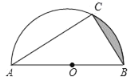
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ���CAB��30����AC��3![]() ����ͼ����Ӱ���ֵ�����ǣ�������
����ͼ����Ӱ���ֵ�����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
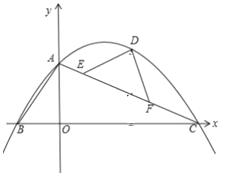
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬ֱ��y����![]() x+4��x���ڵ�C����y���ڵ�A����A��C�����������y��ax2+bx+4��x�Ḻ�����ڵ�B����tan��BAO��
x+4��x���ڵ�C����y���ڵ�A����A��C�����������y��ax2+bx+4��x�Ḻ�����ڵ�B����tan��BAO��![]() ��
��
��1���������ߵĽ���ʽ��
��2����֪E��F���߶�AC������A��C�������㣬��AE��AF��EF��2![]() ��DΪ�������ϵ�һ������һ�㣬��DE��DF�����D�ĺ�����Ϊm����DEF�����ΪS����S��m�ĺ�����ϵʽ����Ҫ��д���Ա���m��ȡֵ��Χ����
��DΪ�������ϵ�һ������һ�㣬��DE��DF�����D�ĺ�����Ϊm����DEF�����ΪS����S��m�ĺ�����ϵʽ����Ҫ��д���Ա���m��ȡֵ��Χ����
��3���ڣ�2���������£�����EDF��90��ʱ������BD��PΪ��������һ���㣬��P��PQ��BD���߶�BD�ڵ�Q������EQ�����P�ĺ�����Ϊt����tΪ��ֵʱ��PE��QE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��ÿ���۸�Ϊ100Ԫ������Ʒ�����̳��������֣����۵���x(Ԫ/��)��ÿ��������y(��)֮��������ͼ��ʾ�Ĺ�ϵ��

(1)���y��x֮��ĺ�����ϵʽ��
(2)д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ���������̳������ˣ��Ὣ�ۼ۶�Ϊ���٣�����֤ÿ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
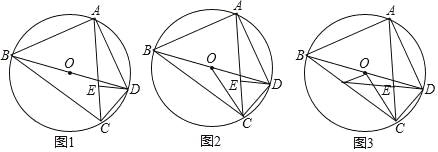
����Ŀ����ͼ���ı���![]() Ϊ
Ϊ![]() ���ڽ��ı��Σ�����
���ڽ��ı��Σ�����![]() ��
��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() �ڵ�
�ڵ�![]() ��
��
(1)��ͼ����֤��![]() ��
��
(2)��ͼ������![]() ����
����![]() ʱ����֤��
ʱ����֤��![]() ��
��
(3)��ͼ����(2)�������£��ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
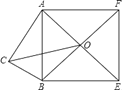
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬AC��5����ABΪһ��������������������ABEF�������ε�����ΪO��![]() ����BC�ߵij�Ϊ_��
����BC�ߵij�Ϊ_��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
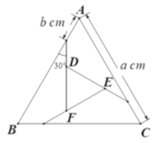
����Ŀ����ͼ���ѱ߳�Ϊ![]() cm�ĵȱ�
cm�ĵȱ�![]() �����IJ��֣���������������������bcm������30����¼�����ʹ�м䲿���γ�һ��С�ĵȱ�
�����IJ��֣���������������������bcm������30����¼�����ʹ�м䲿���γ�һ��С�ĵȱ�![]() .��
.��![]() �������
�������![]() ��
��![]() ����
����![]() ��ֵΪ_____.
��ֵΪ_____.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com