
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() /
/![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以
以![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,当有一点到达终点时,另一点也停止运动,以
运动,当有一点到达终点时,另一点也停止运动,以![]() 、
、![]() 为邻边作设
为邻边作设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]()
![]() 点
点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 在
在![]() 边上时,求
边上时,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ,并写出自变量
,并写出自变量![]() 的取值范围.
的取值范围.
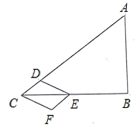
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)根据动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以
以![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,得出
运动,得出![]() ,即可表达出AE的表达式;
,即可表达出AE的表达式;
(2)由![]() ,可得
,可得![]() ,可得
,可得![]() ,列出方程即可求解;
,列出方程即可求解;
(3))分当![]() 时,当
时,当![]() 时,当
时,当![]() 时,三种情况进行画图解答即可.
时,三种情况进行画图解答即可.
解:(1)当点![]() 在
在![]() 边上时,
边上时,![]() ,
,
∴![]()
∴![]() .
.
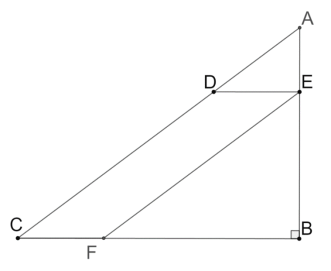
(2)如图:当点![]() 落在线段
落在线段![]() 上时,此时:
上时,此时:![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
在![]() 中:
中:![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
解得![]() .
.
(3)依题意得:![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
当![]() 时,此时E在CB边上,此时
时,此时E在CB边上,此时![]()
如图:过D作DM⊥BC于M
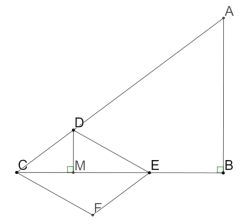
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
当![]() 时,E在AB边上,F在BC的下方,此时:
时,E在AB边上,F在BC的下方,此时:![]()
如图:过E作EP⊥AC于E, EF交BC于Q,连接CE
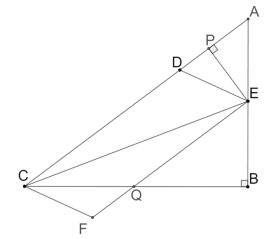
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
在![]() 中EQ//AC
中EQ//AC
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
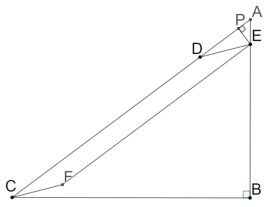
当![]() 时,E在AB边上,F在BC的上方,此时:
时,E在AB边上,F在BC的上方,此时:![]()
如图:过E作EP⊥AC于E,
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴综上所述:![]() 与
与![]() 之间的函数关系式是:
之间的函数关系式是: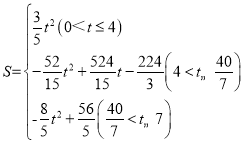


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
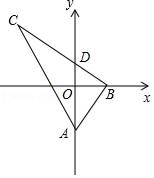
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 经过直线
经过直线![]() 与坐标轴的两个交点
与坐标轴的两个交点![]() .此抛物线与
.此抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() .抛物线的顶点为
.抛物线的顶点为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() .使
.使![]() 与
与![]() 的面积相等?若存在,求点
的面积相等?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图中,每个正方形有边长为1 的小正方形组成:
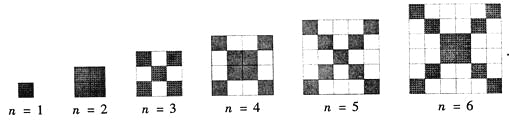
(1) 观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 | … |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
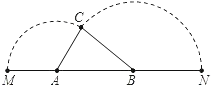
【题目】已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,请解答:(1)x的取值范围______;
(2)若△ABC是直角三角形,则x的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我国建立了比较完善的经济困难学生资助体系.某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为![]() ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com