
如图,设抛物线C1: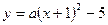 , C2:
, C2: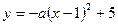 ,C1与C2的交点为A,
,C1与C2的交点为A,
B,点A的坐标是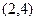 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求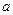 的值及点B的坐标;
的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为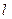 ,且
,且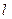 与x轴交于点N.
与x轴交于点N.
①若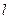 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
②若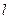 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.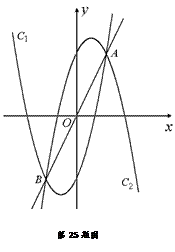
解:(1 )∵点A
)∵点A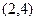 在抛物线C1上,
在抛物线C1上,
∴把点A坐标代入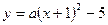 得
得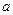 ="1" ……………………………………(2分)
="1" ……………………………………(2分)
∴抛物线C1的解析式为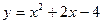
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) …………………………(3分)
(2)①如图1: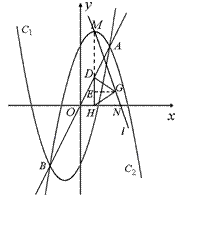
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴点M在DH上,MH="5."
过点G作GE⊥DH,垂足为E ,
,
由△DHG是正三角形,可得EG=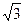 , EH=1,
, EH=1,
∴ ME=4. ………………………………(4分)
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得 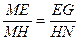 ,
,
∴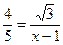 , ∴
, ∴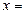
 …………(5分))
…………(5分))
∴点N的横坐标为 .
.
②当点D 移到与点A重合时,如图2,
移到与点A重合时,如图2,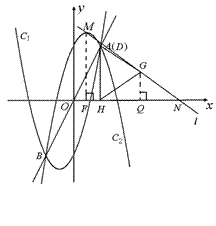
直线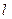 与
与 DG交于点G,此时点N的横坐标最大.
DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F,
设N (x,0)
(x,0)
∵ A (2, 4) ∴ G (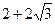 , 2)
, 2)
∴ NQ=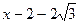 NF =
NF =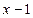 GQ="2 " MF =5.
GQ="2 " MF =5.
∵△NGQ∽△NMF
∴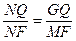
∴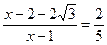
∴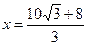 . ………………………………………………………(7分)
. ………………………………………………………(7分)
当点D移到与点B重合时,如图3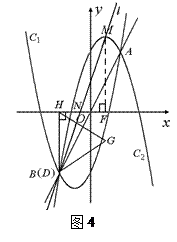
直线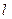 与DG交于点D,即点B
与DG交于点D,即点B
此时点N的横坐标最小.
∵ B(-2, -4) ∴ H(-2, 0), D(-2, -4)
设N(x,0)
∵△BHN∽△MFN,∴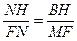
∴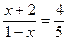 ∴
∴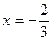

∴点N横坐标的范围为 ≤x≤
≤x≤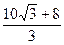 ………………………………(8分)
………………………………(8分)
解析


科目:初中数学 来源: 题型:
 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N.查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(30):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(27):23.5 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年河北省中考考试说明试题汇总卷(二)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年北京市怀柔区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com