
【题目】在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(Ⅰ)当抛物线经过点A时,求顶点P的坐标;
(Ⅱ)若点P在x轴下方,当∠AOP=45°时,若函数值y>0,求对应自变量x的取值范围;
(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.
【答案】(Ⅰ)顶点P(﹣![]() ,﹣
,﹣![]() );(Ⅱ)当函数值y>0,对应自变量x的取值范围为x<5﹣
);(Ⅱ)当函数值y>0,对应自变量x的取值范围为x<5﹣![]() 或x>5+
或x>5+![]() ;(Ⅲ)抛物线解析式为y=x2﹣
;(Ⅲ)抛物线解析式为y=x2﹣![]() x+
x+![]() 或y=x2﹣
或y=x2﹣![]() x+
x+![]() .
.
【解析】
(Ⅰ)把点A代入抛物线解析式求得m,将抛物线配方成顶点式即求得P的坐标.
(Ⅱ)由点P在x轴下方,当∠AOP=45°得点P在直线y=x上.把抛物线配方得用m表示的点P坐标,代入y=x即求得m的值.令抛物线y=0解方程求得抛物线与x轴两交点坐标,由图象可知,在抛物线两侧有函数值y>0,即得到x的取值范围.
(Ⅲ)发现当x=2时,y=4,所以定点H(2,4).过点AA作AB⊥PH于点B,过点B作DC⊥x轴于点C,过点H作HD⊥CD于点D,构造△ABC≌△BHD,利用对应边AC=BD,BC=HD求点B坐标,再求直线BH解析式,把点用m表示的点P坐标代入BH解析式即求得m的值.由于满足∠AHP=45°的点P可以在AH左侧或右侧,故需分情况讨论.
(Ⅰ)把A(1,0)代入y=x2+mx﹣2m得:
1+m﹣2m=0,解得:m=1
∴抛物线解析式为y=x2+x﹣2=(x+![]() )2﹣
)2﹣![]()
∴顶点P(﹣![]() ,﹣
,﹣![]() ),
),
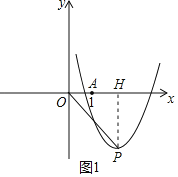
(Ⅱ)过P作PH⊥x轴于点H,如图1
∵点P在x轴下方且∠AOP=45°
∴△POH是等腰直角三角形,P在第四象限
∴OH=PH,
∵y=x2+mx﹣2m=(x+![]() )2﹣
)2﹣![]() ﹣2m
﹣2m
∴P(﹣![]() ,﹣
,﹣![]() ﹣2m)(m<0)
﹣2m)(m<0)
∴﹣![]() =
=![]() +2m
+2m
解得:m1=0(舍去),m2=﹣10
∴抛物线解析式为y=x2﹣10x+20
当y=0时,解得:x1=5﹣![]() ,x2=5+
,x2=5+![]()
由图象可知,当函数值y>0,对应自变量x的取值范围为x<5﹣![]() 或x>5+
或x>5+![]() .
.
(Ⅲ)当x=2时,y=4+2m﹣2m=4
∴无论m取何值,该抛物线都经过定点H(2,4)
过点A作AB⊥PH于点B,过点B作DC⊥x轴于点C,过点H作HD⊥CD于点D,
∴∠ABH=∠ACB=∠BDH=90°
∴∠ABC+∠DBH=∠ABC+∠BAC=90°
∴∠BAC=∠DBH
∵∠AHP=45°
∴△ABH是等腰直角三角形,AB=BH
在△ABC与△BHD中
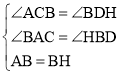
∴△ABC≌△BHD(AAS)
∴AC=BD,BC=HD
设点B坐标为(a,b)
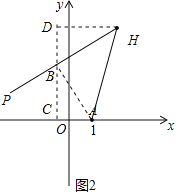
①若点P在AH左侧,即点B在AH左侧,如图2
∴AC=1﹣a,BC=b,BD=4﹣b,DH=2﹣a
∴![]() 解得:
解得: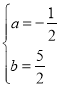
∴点B(﹣![]() ,
,![]() )
)
设直线BH解析式为y=kx+h
∴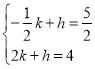 解得:
解得: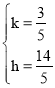
∴直线BH:y=![]() x+
x+![]()
∵点P(﹣![]() ,﹣
,﹣![]() ﹣2m)在直线BH上
﹣2m)在直线BH上
∴![]() (﹣
(﹣![]() )+
)+![]() =﹣
=﹣![]() ﹣2m
﹣2m
解得:m1=﹣![]() ,m2=﹣4
,m2=﹣4
∵m=﹣4时,P(2,4)与点H重合,要舍去
∴抛物线解析式为y=x2﹣![]() x+
x+![]() ,
,
②若点P在AH右侧,即点B在AH右侧,如图3
∴AC=a﹣1,BC=b,BD=4﹣b,DH=a﹣2
∴![]() 解得:
解得:![]()
∴点B(![]() ,
,![]() )
)
设直线BH解析式为y=kx+h
∴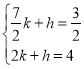 解得:
解得: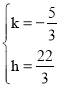
∴直线BH:y=﹣![]() x+
x+![]()
∵点P(﹣![]() ,﹣
,﹣![]() ﹣2m)在直线BH上
﹣2m)在直线BH上
∴﹣![]() ×(﹣
×(﹣![]() )+
)+![]() =﹣
=﹣![]() ﹣2m
﹣2m
解得:m1=﹣![]() ,m2=﹣4(舍去)
,m2=﹣4(舍去)
∴抛物线解析式为y=x2﹣![]() x+
x+![]()
综上所述,抛物线解析式为y=x2﹣![]() x+
x+![]() 或y=x2﹣
或y=x2﹣![]() x+
x+![]() .
.



 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
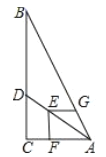
【题目】如图,在 RtABC 中, ACB 90 , AC 6 , BC 12 ,点 D 在边 BC 上,点 E在线段 AD 上, EF AC 于点 F , EG EF 交 AB 于点 G .若 EF EG ,则 CD 的长为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
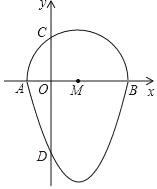
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的直角边OB在x轴上,OB=2,AB=1,将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO,抛物线y=﹣![]() +bx+c经过A,C两点.
+bx+c经过A,C两点.
(1)求点A,C的坐标;
(2)求二次函数的解析式;
(3)连接AC,点P是抛物线上一点,直线OP把△AOC的周长分成相等的两部分,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游团到永定土楼观光,计划购买A型、B型两种型号的土楼模型.若购买8个A型土楼模型和5个B型土楼模型需用1540元;若购买4个A型土楼模型和6个B型土楼模型需用1120元.求A,B两种型号土楼模型的单价分别是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
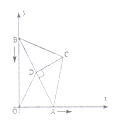
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的高,点
边的高,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限,若
在第一象限,若![]() 从原点出发,沿
从原点出发,沿![]() 轴向右以每秒1个单位长的速度运动,则点
轴向右以每秒1个单位长的速度运动,则点![]() 随之沿
随之沿![]() 轴下滑,并带动
轴下滑,并带动![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒,当
秒,当![]() 到达原点时停止运动
到达原点时停止运动
(1)连接![]() ,线段
,线段![]() 的长随
的长随![]() 的变化而变化,当
的变化而变化,当![]() 最大时,
最大时,![]() ______.
______.
(2)当![]() 的边与坐标轴平行时,
的边与坐标轴平行时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
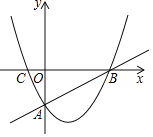
【题目】如图,直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣
x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣![]() x+c经过A,B两点,与x轴的另一交点为C.
x+c经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)M为抛物线上一点,直线AM与x轴交于点N,当![]() 时,求点M的坐标;
时,求点M的坐标;
(3)P为抛物线上的动点,连接AP,当∠PAB与△AOB的一个内角相等时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com