
【题目】如图1,![]() ,
,![]() 是线段
是线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边,在
为边,在![]() 的同侧构造菱形
的同侧构造菱形![]() 和菱形
和菱形![]() ,
,![]() 三点在同一条直线上连结
三点在同一条直线上连结![]() ,设射线
,设射线![]() 与射线
与射线![]() 交于
交于![]() .
.
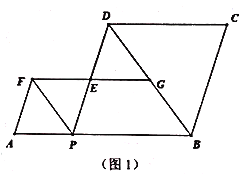
(1)当![]() 在点
在点![]() 的右侧时,求证:四边形
的右侧时,求证:四边形![]() 是平形四边形.
是平形四边形.
(2)连结![]() ,当四边形
,当四边形![]() 恰为矩形时,求
恰为矩形时,求![]() 的长.
的长.
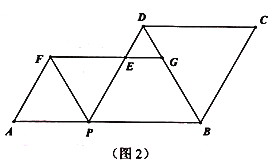
(3)如图2,设![]() ,
,![]() ,记点
,记点![]() 与
与![]() 之间的距离为
之间的距离为![]() ,直接写出
,直接写出![]() 的所有值.
的所有值.
【答案】(1)见解析;(2)FG=![]() ;(3)d=14或
;(3)d=14或![]() .
.
【解析】
(1)由菱形的性质可得AP∥EF,∠APF=∠EPF=![]() ∠APE,PB∥CD,∠CDB=∠PDB=
∠APE,PB∥CD,∠CDB=∠PDB=![]() ∠CDP,由平行线的性质可得∠FPE=∠BDP,可得PF∥BD,即可得结论;
∠CDP,由平行线的性质可得∠FPE=∠BDP,可得PF∥BD,即可得结论;
(2)由矩形的性质和菱形的性质可得FG=PB=2EF=2AP,即可求FG的长;
(3)分两种情况讨论,由勾股定理可求d的值;点G在DP的右侧,连接AC,过点C作CH⊥AB,交AB延长线于点H;若点G在DP的左侧,连接AC,过点C作CH⊥AB,交AB延长线于点H.
(1)∵四边形APEF是菱形
∴AP∥EF,∠APF=∠EPF=![]() ∠APE,
∠APE,
∵四边形PBCD是菱形
∴PB∥CD,∠CDB=∠PDB=![]() ∠CDP
∠CDP
∴∠APE=∠PDC
∴∠FPE=∠BDP
∴PF∥BD,且AP∥EF
∴四边形四边形FGBP是平形四边形;
(2)若四边形DFPG恰为矩形
∴PD=FG,PE=DE,EF=EG,
∴PD=2EF
∵四边形APEF是菱形,四边形PBCD是菱形
∴AP=EF,PB=PD
∴PB=2EF=2AP,且AB=10
∴FG=PB=![]() .
.
(3)如图,点G在DP的右侧,连接AC,过点C作CH⊥AB,交AB延长线于点H,

∵FE=2EG,
∴PB=FG=3EG,EF=AP=2EG
∵AB=10
∴AP+PB=5EG=10
∴EG=2,
∴AP=4,PB=6=BC,
∵∠ABC=120°,
∴∠CBH=60°,且CH⊥AB
∴BH=![]() BC=3,CH=
BC=3,CH=![]() BH=3
BH=3![]()
∴AH=13
∴AC=![]() =14
=14
若点G在DP的左侧,连接AC,过点C作CH⊥AB,交AB延长线于点H

∵FE=2EG,
∴PB=FG=EG,EF=AP=2EG
∵AB=10,
∴3EG=10
∴EG=![]()
∴BP=BC=![]()
∵∠ABC=120°,
∴∠CBH=60°,且CH⊥AB
∴BH=![]() BC=
BC=![]() ,CH=
,CH=![]() BH=
BH=![]()
∴AH=![]()
∴AC=![]()
综上所述:d=14或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,已知两批文具的售价均为每件15元.
(1)第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
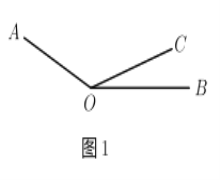
【题目】如图![]() ,已知
,已知![]() ,
,![]() 且
且![]() 、
、![]() 满足等式
满足等式![]() ,射线
,射线![]() 从
从![]() 处绕点
处绕点![]() 以
以![]() 度秒的速度逆时针旋转.
度秒的速度逆时针旋转.
(1)试求∠AOB的度数.
(2)如图![]() ,当射线
,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从
从![]() 处以
处以![]() 度/秒的速度绕点
度/秒的速度绕点![]() 顺时针旋转,当他们旋转多少秒时,使得
顺时针旋转,当他们旋转多少秒时,使得![]() ?
?
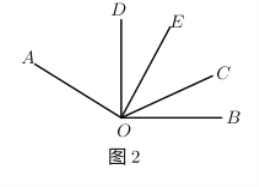
(3)如图![]() ,若射线
,若射线![]() 为
为![]() 的平分线,当射线
的平分线,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从射线
从射线![]() 处以
处以![]() 度秒的速度绕点
度秒的速度绕点![]() 顺时针旋转,使得这两条射线重合于射线
顺时针旋转,使得这两条射线重合于射线![]() 处(
处(![]() 在
在![]() 的内部)时,且
的内部)时,且![]() ,试求
,试求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
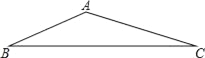
A. 450a元 B. 225a元 C. 150a元 D. 300a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
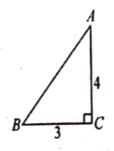
【题目】如图,一张三角形纸片![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,现小林将纸片做三次折叠:第一次使点
,现小林将纸片做三次折叠:第一次使点![]() 落在
落在![]() 处;将纸片展平做第二次折叠,使点
处;将纸片展平做第二次折叠,使点![]() 若在
若在![]() 处;再将纸片展平做第三次折叠,使点
处;再将纸片展平做第三次折叠,使点![]() 落在
落在![]() 处,这三次折叠的折痕长依次记为
处,这三次折叠的折痕长依次记为![]() ,则
,则![]() 的大小关系是(从大到小)__________.
的大小关系是(从大到小)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)(-2a3)23a3+6a12÷(-2a3);
(3)(x+1)(x-2)-(x-2)2;
(4)(a+2b+3)(a+2b-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com