
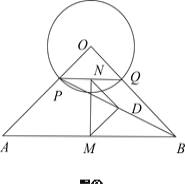
【题目】如图本题图①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,以
上一点,以![]() 为半径作
为半径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,线段
,线段![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() .
.
(1)试探究![]() 是什么特殊三角形?说明理由;
是什么特殊三角形?说明理由;
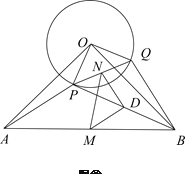
(2)将![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
(3)若![]() ,把
,把![]() 绕点
绕点![]() 在平面内自由旋转,求
在平面内自由旋转,求![]() 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.
【答案】(1)![]() 为等腰直角三角形;(2)
为等腰直角三角形;(2)![]() 仍然为等腰直角三角形;(3)
仍然为等腰直角三角形;(3)![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()
【解析】分析:(1)由OA=OB,OP=OQ可得AP=BQ,再利用三角形的中位线可得△DMN是等腰直角三角形;
(2)由旋转的性质得∠AOP=∠BOQ,从而可证△AOP≌△BOQ,由三角形中位线的性质可得DM=DN,根据平行线的性质和三角形内角和可证∠MDN=90°,从而结论得证;
(3)如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .由三角形三边的关系得
.由三角形三边的关系得![]() ,
,![]() ,由三角形的面积公式得
,由三角形的面积公式得![]() ,从而可求出y的最大值和最小值,然后相减即可.
,从而可求出y的最大值和最小值,然后相减即可.
详解:(1)![]() 为等腰直角三角形
为等腰直角三角形
![]()
![]() 分别为
分别为![]() 的中点,
的中点,
![]()
![]() 且
且![]()
同理:![]()
![]()
![]()
![]()
![]() .
.
又![]()
![]()
![]()
![]() 即
即![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图,![]() 仍然为等腰直角三角形.
仍然为等腰直角三角形.
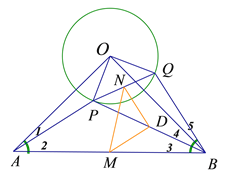
证明:由旋转的性质,![]() .
.
![]()
![]()
![]()
![]() ≌
≌![]() ,
,
![]()
![]() .
.
![]()
![]() 分别为
分别为![]() 的中点,
的中点,![]()
![]() 且
且![]()
同理:![]() ,
,![]()
![]()
在等腰Rt![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]() 同理:
同理:![]()
![]()
![]()
=![]()
![]() .
.
![]()
![]()
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
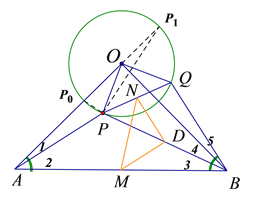
(3), 如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
连接![]()
![]() ,而
,而![]() ,
,
![]() 同理,
同理,![]()
由题意,![]() ,
,
![]()
![]() 的最小值为
的最小值为![]() . 同理,
. 同理,![]() 最大值为
最大值为![]() ,
,
从而得![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
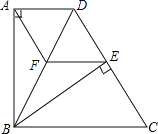
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值5.
时,函数有最大值5.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线![]() 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为![]() ,当以
,当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,求
轴相切时,求![]() 的值.
的值.
(3)若点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程![]() 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.

(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com