
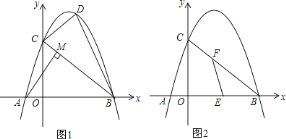
����Ŀ����ͼ![]() ����ƽ��ֱ������ϵ�У�ֱ��
����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �Ḻ������һ�㣬
�Ḻ������һ�㣬![]() �ڵ�
�ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����֪������
����֪������![]() ������
������![]() ��
��![]() ��
��![]() ��
��
![]() �������ߵĺ�����ϵʽ��
�������ߵĺ�����ϵʽ��
![]() ����
����![]() ����
����![]() ���߶�
���߶�![]() �Ϸ����������ϣ�����
�Ϸ����������ϣ�����![]() ��
��![]() ����
����![]() ��
��![]() �������
�������![]() �����
�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ
��ͼ![]() ��
��![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣨�����˵㣩������
��һ�㣨�����˵㣩������![]() ��һ����
��һ����![]() ��
��![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() ��ֹͣ������
��ֹͣ������![]() �������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��
�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��![]() �����꣮
�����꣮
���𰸡���1��![]() ��2��
��2��![]() ��
��![]() ��3����
��3����![]() �������˶����������õ�����ʱ��
�������˶����������õ�����ʱ��![]() �룬��ʱ��
�룬��ʱ��![]() ������Ϊ
������Ϊ![]()
��������
��1��������OC=3��4CN=5ON�����ON=![]() ����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A��-1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=-
����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A��-1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=-![]() x2+
x2+![]() x+3��
x+3��
��2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=-![]() x+3����PQ��y�ύBC��Q����ͼ1����P��x��-
x+3����PQ��y�ύBC��Q����ͼ1����P��x��-![]() x2+
x2+![]() x+3������Q��x��-
x+3������Q��x��-![]() x+3�����ټ����DQ=-
x+3�����ټ����DQ=-![]() x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=-
x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=-![]() x2+6x��Ȼ�����S��BCD=
x2+6x��Ȼ�����S��BCD=![]() S��ABC�õ�-
S��ABC�õ�-![]() x2+6x=
x2+6x=![]() ��
��![]() ����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ
����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ
��3����F��m��-![]() x+3�����������ľ��빫ʽ�õ�EF=
x+3�����������ľ��빫ʽ�õ�EF=![]() ��CF=
��CF=![]() x�����P�������˶�����������ʱ��t=EF+
x�����P�������˶�����������ʱ��t=EF+![]() =EF+
=EF+![]() CF�����ݲ���ʽ��ʽ�õ�EF+
CF�����ݲ���ʽ��ʽ�õ�EF+![]() CF��
CF��![]() ����EF=
����EF=![]() CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��
CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��![]() x2-
x2-![]() x+13=��
x+13=��![]()
![]() x��2��x1=2��x2=
x��2��x1=2��x2=![]() ����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��
����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2��![]() ����
����
![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
��![]() ��
��
�������߽���ʽΪ![]() ��
��
��![]() �����
�����![]() �����
�����![]() ��
��
�������߽���ʽΪ![]() ��
��![]() ��ֱ��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() ��
��![]() �����
�����![]() �����
����� ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �ύ
�ύ![]() ��
��![]() ����ͼ
����ͼ![]() ����
����![]() ����
����![]() ��
��
![]() ��
��
��![]()
![]() ��
��
��![]() ��
��
��![]() ��
��
������![]() �����
�����![]() ��
��![]() ��
��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��![]() �������˶�����������ʱ��
�������˶�����������ʱ��![]() ����
����![]() ʱ��ȡ�Ⱥţ���ʱ
ʱ��ȡ�Ⱥţ���ʱ![]() ��С��
����
��![]() ��
��
������![]() �����
�����![]() ��
��![]() ����ȥ����
����ȥ����
���![]() �������˶����������õ�����ʱ��
�������˶����������õ�����ʱ��![]() �룬��ʱ��
�룬��ʱ��![]() ������Ϊ
������Ϊ![]() ��
��


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
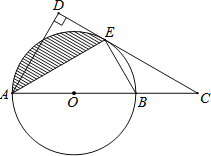
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��AB�ӳ�����һ�㣬CD���O�����ڵ�E��AD��CD�ڵ�D��
��1����֤��AEƽ�֡�DAC��
��2����AB=4����ABE=60�㣬���ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() �IJ���ͼ����ͼ��ʾ��ͼ�����
�IJ���ͼ����ͼ��ʾ��ͼ�����![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() �����н��ۣ���1��
�����н��ۣ���1��![]() ����2��
����2��![]() ����3������
����3������![]() ����
����![]() ����
����![]() �ڸú���ͼ���ϣ���
�ڸú���ͼ���ϣ���![]() ����4��������
����4��������![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() ����
����![]() ��������ȷ���۵������________.
��������ȷ���۵������________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
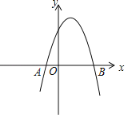
����Ŀ����ͼ����AOB��ֱ�������Σ���AOB=90�㣬OB=2OA����A�ڷ���������y=![]() ��ͼ���ϣ�����B�ڷ���������y=
��ͼ���ϣ�����B�ڷ���������y=![]() ��ͼ���ϣ���k��ֵΪ�� ��
��ͼ���ϣ���k��ֵΪ�� ��

A��-4 B��4 C��-2 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����ͼ��ʾ��������˵����
��ͼ����ͼ��ʾ��������˵����![]() ����
����![]() ���۵�
���۵�![]() ʱ��
ʱ��![]() ���ܵ�
���ܵ�![]() ʱ��
ʱ��![]() ���ݹ���
���ݹ���![]() ��һԪ���η���
��һԪ���η���![]() ����������ȵ�ʵ����������Ϊ������ȷ���У� ��
����������ȵ�ʵ����������Ϊ������ȷ���У� ��
A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ֽƬABC�У���C=90����AB=12��BC=6��B���DZ�AC��һ�㣮��������ֽƬ�۵���ʹ��B���B���غϣ��ۺ���BC��AB�ֱ��ཻ��E��F����BE=x��
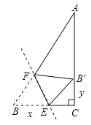
��1����x=4����B��C�ij���
��2������AFB����ֱ��������ʱ�����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x+m��1=0������ʵ����x1��x2��
��1����m��ȡֵ��Χ��
��2����x12+x22=6x1x2ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
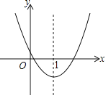
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=��x2+2x+3��x�ύ��A��B���㣬��M�������������ϣ���P��y���ϣ�����ı���ABMP��ƽ���ı��Σ����M������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ������ȫ�������������ƺţ���ĩ����ί��֯־Ը�߽��������������������ʦ������4��Ů��ɲ���С�á�С�ݡ�С��Сٻ����ͨ����ǩ��ʽȷ��2��Ů��ȥ�μӣ���ǩ����4��Ů��ɲ������ֱ�д��4����ȫ��ͬ�Ŀ�Ƭ���棬�����ſ�Ƭ���泯�ϣ�ϴ�Ⱥ���������ϣ�����ʦ�ȴ��������ȡһ�ſ�Ƭ�������������ٴ�ʣ���3�ſ�Ƭ�������ȡ�ڶ��ţ�����������
��1���ð�������С�ձ����������� ���¼�����С�ñ����������� ���¼���������������������Ȼ�����������������һ�γ�ȡ��Ƭ��С�ñ��������ĸ���Ϊ�� ����
��2�����û���״ͼ���б��ķ�����ʾ��γ�ǩ���п��ܵĽ�����������С�ݱ��������ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com