
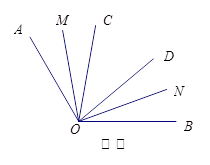
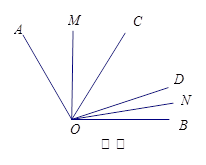
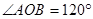 ,
,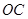 、
、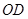 是过点
是过点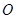 的射线,射线
的射线,射线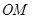 、
、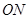 分别平分
分别平分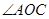 和
和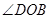 .
.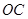 、
、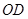 是
是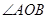 的三等分线,则
的三等分线,则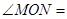 °
°
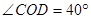 ,
,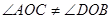 ,则
,则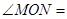 °
°
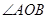 内,若
内,若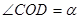 (
(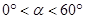 ),则
),则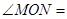 °
°
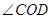 绕着点
绕着点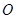 逆时针旋转到
逆时针旋转到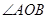 的外部(
的外部(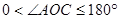 ,
,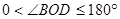 ),求此时
),求此时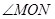 的度数.
的度数. 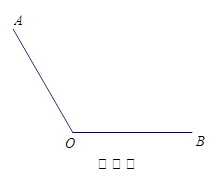
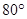 ;(2)
;(2)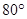 ;(3)
;(3) ;(4)
;(4) 或
或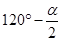
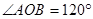 ,
,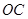 、
、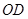 是
是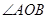 的三等分线,再结合射线
的三等分线,再结合射线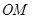 、
、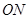 分别平分
分别平分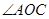 和
和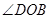 即可求得结果;
即可求得结果;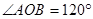 ,
,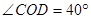 ,可得∠AOC+∠DOB的度数,再根据射线
,可得∠AOC+∠DOB的度数,再根据射线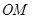 、
、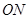 分别平分
分别平分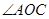 和
和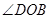 可得∠MOC+∠DON的度数,从而求得结果;
可得∠MOC+∠DON的度数,从而求得结果;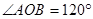 ,
,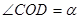 ,可表示∠AOC+∠DOB的度数,再根据射线
,可表示∠AOC+∠DOB的度数,再根据射线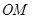 、
、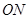 分别平分
分别平分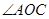 和
和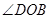 可表示∠MOC+∠DON的度数,从而得到结果;
可表示∠MOC+∠DON的度数,从而得到结果;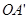 、
、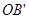 ,分五种情况:①射线OD在
,分五种情况:①射线OD在 内,
内,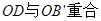 ,③
,③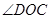 在
在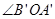 内部,④OC与
内部,④OC与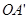 重合,⑤OC在
重合,⑤OC在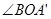 内部,根据三等分线及角平分线的性质分析即可.
内部,根据三等分线及角平分线的性质分析即可.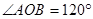 ,
,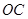 、
、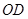 是
是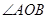 的三等分线
的三等分线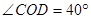
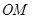 、
、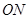 分别平分
分别平分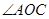 和
和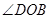
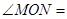 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON=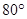 ;
;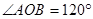 ,
,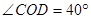
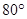
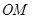 、
、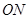 分别平分
分别平分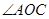 和
和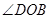
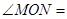 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON=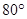 ;
;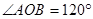 ,
,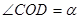
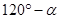
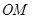 、
、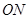 分别平分
分别平分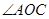 和
和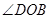
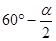
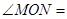 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON= ;
;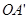 、
、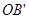
 内
内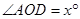 ,则
,则

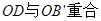


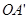 重合
重合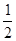 ∠BOD=
∠BOD=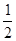 (60º+α)="∠DON"
(60º+α)="∠DON" 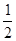 (60º+α)-α=30º-
(60º+α)-α=30º-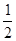 α
α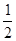 α=60º+
α=60º+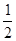 α
α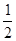 α)=120º-
α)=120º-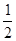 α
α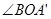 内部
内部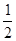 ∠AOC=
∠AOC=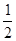 (α+x)
(α+x) 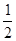 ∠BOD=
∠BOD=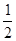 (120º+x)
(120º+x)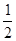 (120º+x)-
(120º+x)-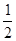 (α+x)=60º+
(α+x)=60º+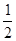 α
α

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题
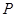 是
是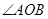 的边
的边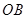 上的一点.
上的一点.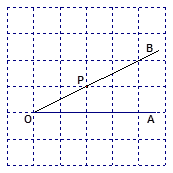
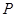 画OB的垂线,交
画OB的垂线,交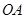 于点C;
于点C;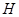 ;
;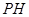 的长度是点
的长度是点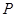 到直线 的距离, 是点
到直线 的距离, 是点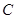 到直线
到直线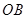 的距离;因为 ,所以线段
的距离;因为 ,所以线段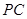 、
、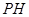 、
、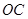 这三条线段大小关系是 (用“<”号连接)
这三条线段大小关系是 (用“<”号连接)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.过一点有且只有一条直线与已知直线平行 |
| B.相等的两个角一定是对顶角 |
| C.将一根细木条固定在墙上,只需要一根钉子 |
| D.同角的余角相等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
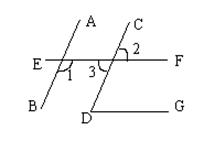
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.45° | B.35° | C.55° | D.125° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com