
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
|
|
| x-1 |
| x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 先阅读理解下面的例题,再按要求解答下列问题:
先阅读理解下面的例题,再按要求解答下列问题:查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建泉州第三中学八年级上学期期中考试数学试题(带解析) 题型:解答题
先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式 的最小值.
的最小值.
解: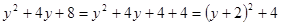


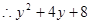 的最小值是
的最小值是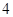 .
.
(1)求代数式 的最小值;
的最小值;
(2)求代数式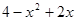 的最大值;
的最大值;
(3)某居民小区要在一块一边靠墙(墙长 m)的空地上建一个长方形花园
m)的空地上建一个长方形花园 ,花园一边靠墙,另三边用总长为
,花园一边靠墙,另三边用总长为 m的栅栏围成. 如图,设
m的栅栏围成. 如图,设 (m),请问:当
(m),请问:当 取何值时,花园的面积最大?最大面积是多少?
取何值时,花园的面积最大?最大面积是多少?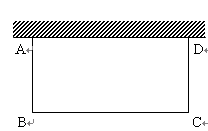
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(广东湛江卷)数学(解析版) 题型:解答题
先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
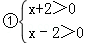
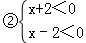
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
(1)一元二次不等式x2﹣16>0的解集为 ;
(2)分式不等式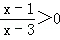 的解集为 ;
的解集为 ;
(3)解一元二次不等式2x2﹣3x<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com