
 ,
, (x-m)2+2m+2;
(x-m)2+2m+2;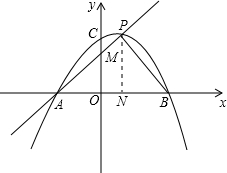
 AO•OM=1,
AO•OM=1, (x-m)2+2m+2=0,
(x-m)2+2m+2=0, •PN•BN=4,
•PN•BN=4, •(2m+2)•(m+1)=4,
•(2m+2)•(m+1)=4, ,
, ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
(本题8分)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线L1,一次函数y=k2x+b2(k2≠0)的图象为直线L2,若k1=k2,且b1≠b2,我们就称直线L1与直线L2互相平行.解答下面的问题:
(1)求过点P(1,4),且与直线y=-2x-1平行的直线L的函数解析式,并画出直线L的图象;
(2)设直线L分别与y轴,x轴交于点A,B,如果直线m:y=kx+t(t>0)与直线L平行,且交x轴于点C,求出△ABC的面积S关于t函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西玉林卷)数学 题型:解答题
(11·漳州)(满分13分)如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.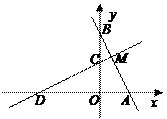
(1)填空:点C的坐标是(_ ▲ ,_  ▲ ),
▲ ),
点D的坐标是(_ ▲ ,_ ▲ );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,
请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江省衢州市实验学校2011-2012学年八年级上学期期末考试数学卷 题型:解答题
(本题8分)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线L1,一次函数y=k2x+b2(k2≠0)的图象为直线L2,若k1=k2,且b1≠b2,我们就称直线L1与直线L2互相平行.解答下面的问题:
(1)求过点P(1,4),且与直线y=-2x-1平行的直线L的函数解析式,并画出直线L的图象;
(2)设直线L分别与y轴,x轴交于点A,B,如果直线m:y=kx+t(t>0)与直线L平行,且交x轴于点C,求出△ABC的面积S关于t函数解析式.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北武汉卷)数学 题型:解答题
(本题满分12分)如图1,抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com