
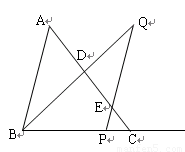
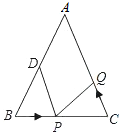
如图,已知△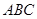 中,
中,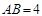 ,
,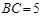 ,
,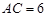 ,把线段
,把线段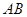 沿射线
沿射线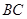 方向平移至PQ,直线PQ与直线AC交于点E,又联结BQ与直线AC交于点D.
方向平移至PQ,直线PQ与直线AC交于点E,又联结BQ与直线AC交于点D.
(1)若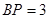 ,求
,求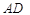 的长;
的长;
(2)设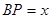 ,
,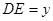 ,试求y关于x的函数解析式;
,试求y关于x的函数解析式;
(3)当 为多少时,以Q、D、E为顶点的三角形与
为多少时,以Q、D、E为顶点的三角形与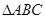 相似.
相似.
解:(1)联结AQ
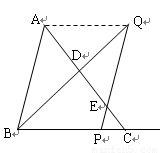
∵AB∥PQ AB=PQ
∴AQ∥BP AQ=BP
∵BP=3
∴AQ=3
∵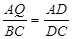
∴
∴
(2) ∵AB∥PQ,AQ∥BC
∴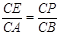 ,
,
∵ ,
, ,
, ,
, ,
,
当点P在边BC上时,
∴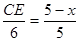 , 解得
, 解得
 , 解得
, 解得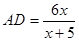
∴ 
当点P在边BC的延长线上时,

∴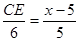 , 解得
, 解得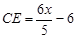
 , 解得
, 解得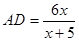
∴ 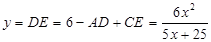
综上, (
( )
)
(3)∵AB∥PQ,∴△EDQ∽△ADB
又以Q、D、E为顶点的三角形与 相似,
相似,
∴△ADB与 相似
相似
∵∠BAC公共,又∠ABD≠∠ABC
∴ ∠ABD=∠ACB
∴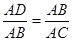 即
即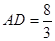
由(2)知,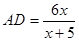
∴  得
得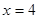
所以,当 为4时,以Q、D、E为顶点的三角形与
为4时,以Q、D、E为顶点的三角形与 相似.
相似.
【解析】(1)连接AQ,由平行四边形的判定定理可得出四边形ABPQ是平行四边形,进而可得出△ADQ∽△CDB,由相似三角形的对应边成比例即可得出结论;
(2)由平行线分线段成比例定理可知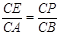 ,
, ,再根据点P在边BC上或点P在边BC的延长线上两种情况讨论即可;
,再根据点P在边BC上或点P在边BC的延长线上两种情况讨论即可;
(3)先由相似三角形的判定定理得出△EDQ∽△ADB,△ADB∽△ABC,由相似三角形的对应边成比例即可求出BP的长.


科目:初中数学 来源: 题型:
 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=
34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.
如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证:
如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com