
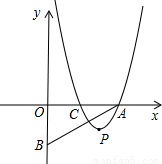
 ab=
ab= ��m+2-n��n����ɵõ�m+2=2nʱ��S��AOB���
��m+2-n��n����ɵõ�m+2=2nʱ��S��AOB���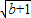 ��b����E��n+1+
��b����E��n+1+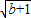 ��b�������F����Ϊ��x��y�����������y��ֵ�����F��б��DE�ľ���Ϊb-��b-1��=1������P��б��AC����һ��������֤��ԭ��������ȷ�ģ�
��b�������F����Ϊ��x��y�����������y��ֵ�����F��б��DE�ľ���Ϊb-��b-1��=1������P��б��AC����һ��������֤��ԭ��������ȷ�ģ� ab=
ab= ��m+2-n��n��
��m+2-n��n�� [
[ ��m+2-n��+n]2=
��m+2-n��+n]2= ��m+2��2��
��m+2��2�� ��m+2��]2-
��m+2��]2- ��m+2��2+n��m+2-n����
��m+2��2+n��m+2-n���� ��m+2��2-n��m+2-n��]=��m+2-n��-n��
��m+2��2-n��m+2-n��]=��m+2-n��-n��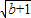 ��b����E��n+1+
��b����E��n+1+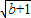 ��b����
��b����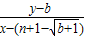 •
•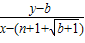 =-1��
=-1��

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
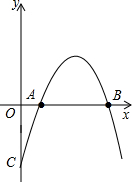 ���κ���y=ax2+bx+c��a��0����ͼ����A��B����y���ཻ�ڵ�C��
���κ���y=ax2+bx+c��a��0����ͼ����A��B����y���ཻ�ڵ�C��| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�㽭һģ����ͼ����֪��ƽ��ֱ������ϵ�У���A��4��0����B��-3��0������C��y���������ϣ���tan��CAO=1����Q���߶�AB�ϵĶ��㣬����Q��QE��AC��BC�ڵ�E��
��2013•�㽭һģ����ͼ����֪��ƽ��ֱ������ϵ�У���A��4��0����B��-3��0������C��y���������ϣ���tan��CAO=1����Q���߶�AB�ϵĶ��㣬����Q��QE��AC��BC�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
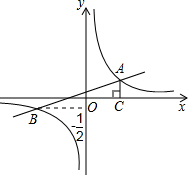 ��2012•������ģ�⣩��ͼ����֪��ƽ��ֱ������ϵxOy�У�һ�κ���y1=kx+b��k��0����ͼ���뷴��������y2=
��2012•������ģ�⣩��ͼ����֪��ƽ��ֱ������ϵxOy�У�һ�κ���y1=kx+b��k��0����ͼ���뷴��������y2=| m |
| x |
| 1 |
| 2 |
| m |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com