
【题目】去年11月,体质监测中心有关专家随机抽查了我市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
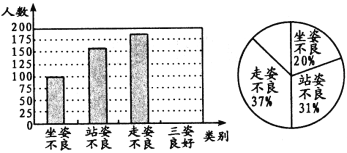
(1)请将两幅统计图补充完整;
(2)一共抽查了多少名学生?
(3)如果我市有10万名初中生,那么我市初中生中,三姿良好的学生约有多少人?
(4)根据统计结果,请你简单谈谈自己的看法.
【答案】(1)详见解析;(2)500;(3)1.2万;(4)答案不唯一,要点:中学生要坚持锻炼身体,努力纠正坐立、行走中的不良习惯,促进身心健康发展
【解析】
(1)先根据直方图数据和扇形图各百分比求出样本,再求出三姿良好的频数与所占比例,最后把统计图补充完整即可.
(2)用”坐姿不良”的频数100除以所占比例![]() 即可得到抽查样本.
即可得到抽查样本.
(3)用10万乘以三姿良好学生所占比例即可.
(4)针对”三姿不良”的情况提出适当建议即可.
解: (1)![]() ,
,
![]() 人,
人,
![]() 人.
人.
:
(2)![]() 人.
人.
所以共抽查了500名学生.
(3)![]() 万人
万人
所以三姿良好的学生约有1.2万人.
(4)答: 中学生要坚持锻炼身体,努力纠正坐立、行走中的不良习惯,促进身心健康发展.


科目:初中数学 来源: 题型:
【题目】在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程![]() =
=![]() 的解为x=
的解为x=![]() ;
;
⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2![]() .
.
正确的序号有( )
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
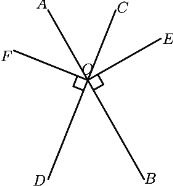
【题目】已知:如图直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]()
(1)图中与![]() 互余的角有 ,图中与
互余的角有 ,图中与![]() 互补的角有 (备注:写出所有符合条件的角)
互补的角有 (备注:写出所有符合条件的角)
(2)根据下列条件,分别求![]() 的度数:①射线
的度数:①射线![]() 平分
平分![]() ;②
;②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
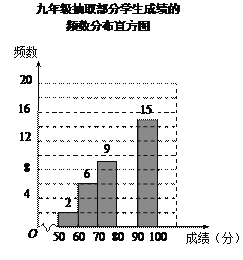
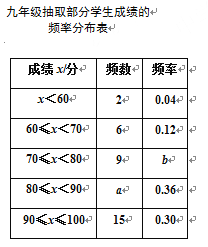
请根据所给信息,解答下列问题:
(1)a=______,b=_______;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小烨在探究数轴上两点间距离时发现:若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() ;若
;若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() .据此,小烨猜想:对于平面内任意两点
.据此,小烨猜想:对于平面内任意两点![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
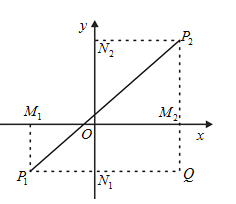
(1)请你利用下图,试证明:;
(2)若![]() ,试在
,试在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 的距离最短,并求出
的距离最短,并求出![]() 的最小值和
的最小值和![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com