
【题目】如图,在每个小正方形的边长均为1的方格纸中,其中端点![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
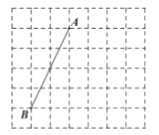
(1)在图中画出平行四边形![]() ,点
,点![]() 和点
和点![]() 均在小正方形的顶点上,且平行四边形
均在小正方形的顶点上,且平行四边形![]() 的面积为12;
的面积为12;
(2)在图中画出以![]() 为腰的等腰直角
为腰的等腰直角![]() ,且点
,且点![]() 在小正方形的顶点上;
在小正方形的顶点上;
(3)连接![]() ,直接写出
,直接写出![]() 的正切值.
的正切值.
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线上的两个动点M、N,满足AB=![]() MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
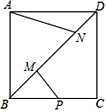
A.4B.2![]() C.6D.3
C.6D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
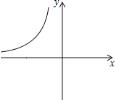
(1)图象的另一支在第________象限;在每个象限内,![]() 随
随![]() 的增大而________;
的增大而________;
(2)常数![]() 的取值范围是________;
的取值范围是________;
(3)若此反比例函数的图象经过点![]() ,求
,求![]() 的值.点
的值.点![]() 是否在这个函数图象上?点
是否在这个函数图象上?点![]() 呢?
呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C(2,![]() )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
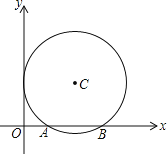
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,顶点
两点,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
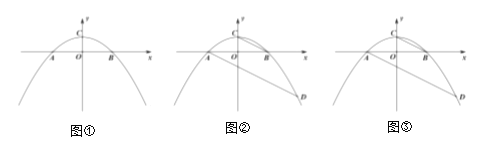
(1)如图①,求抛物线的解析式;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在第四象限的抛物线上,过点
在第四象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
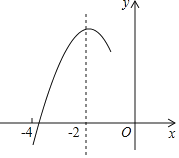
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
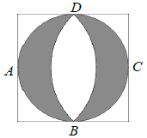
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
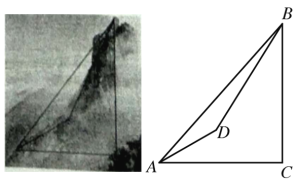
【题目】某学校数学兴趣小组想利用数学知识测量某座山的海拔高度,如图,他们在山腰A处测得山顶B的仰角为45°,他们从A处沿着坡度为i=1 : ![]() 的斜坡前进1000 m到达D处,在D处测得山顶B的仰角为58°,若点A处的海拔为12米,求该座山顶点B处的海拔高度,(结果保留整数,参考数据:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,
的斜坡前进1000 m到达D处,在D处测得山顶B的仰角为58°,若点A处的海拔为12米,求该座山顶点B处的海拔高度,(结果保留整数,参考数据:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,![]() ≈1. 732)
≈1. 732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com