
古希腊的数学家、天文学家、哲学家毕达哥拉斯,对数学的发展作出了卓越的贡献,最著名的是他与他的学生发现并证明了在我国称为“勾股定理”的几何定理,国外称“毕达哥拉斯定理”.据说当他们发现了这一定理后,他与他的学生欣喜若狂,竟杀了100头牛举行盛大庆典,以示庆祝.
一次,有人问毕达哥拉斯有多少学生.他的回答是一道有趣的数学题:我的学生一半在学数学,四分之一学音乐,七分之一沉默无言,此外,还有三名女生.请你算一算,毕达哥拉斯究竟有多少个学生.
科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
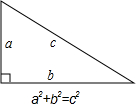 定理”.它揭示了一个直角三角形三条边之间的数量关系(如图).
定理”.它揭示了一个直角三角形三条边之间的数量关系(如图).| 12+12 |
| 2 |
| 12+22 |
| 5 |
| 10 |
| 10 |
| 13 |
| 13 |
查看答案和解析>>
科目:初中数学 来源:鼎尖助学系列—同步练习(数学 七年级下册)、与三角形有关的角 题型:022
古希腊的数学家把数1,3,6,10,15,21…叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
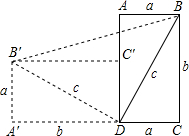
 (a+b)(a+b)=
(a+b)(a+b)= (a+b)2,且又知梯形S梯形A‵B‵BC=S△ABD+S△DBB‵+S△BCD=
(a+b)2,且又知梯形S梯形A‵B‵BC=S△ABD+S△DBB‵+S△BCD= ab+
ab+ c2+
c2+ ab,故有
ab,故有 (a+b)2=
(a+b)2= ab+
ab+ c2+
c2+ ab,则a2+b2+2ab=c2+2ab,即a2+b2=c2.
ab,则a2+b2+2ab=c2+2ab,即a2+b2=c2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com