
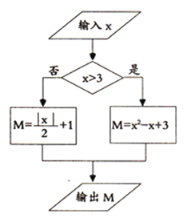
【题目】嘉淇设计了一个如图所示的数值转换程序.
(1)当输入![]() 时,输出
时,输出![]() 的值为 .当输入
的值为 .当输入![]() 时,输出
时,输出![]() 的值为 ;
的值为 ;
(2)若(1)中![]() 的两个数值依次对应数轴上的点
的两个数值依次对应数轴上的点![]() ,
,![]() ,点
,点![]() 为数轴上另外一点,且满足
为数轴上另外一点,且满足![]() ,求点
,求点![]() 对应的数;
对应的数;
(3)当输出![]() 的值为15时,求输入
的值为15时,求输入![]() 的值.
的值.
【答案】(1)3,23;(2) 点C对应的数为-7或8;(3) x的值为-28或4
【解析】
(1)将x=-4代入M=![]() 计算可得;将x=5代入M=x2-x+3计算可得;
计算可得;将x=5代入M=x2-x+3计算可得;
(2)根据题意得:A表示3,B表示23,设C表示x.由AC=![]() BC,列方程求解即可;
BC,列方程求解即可;
(3)分别计算出![]() 1=15和x2-x+3=15中x的值,再根据x的范围取舍即可得到结论.
1=15和x2-x+3=15中x的值,再根据x的范围取舍即可得到结论.
(1)当x=-4时,M=![]() =2+1=3;当x=5时,M=x2-x+3=23;
=2+1=3;当x=5时,M=x2-x+3=23;
(2)根据题意得:A表示3,B表示23,设C表示x.
∵AC=![]() BC,∴3AC=BC,∴3|x-3|=|23-x|,∴3(x-3)=23-x或3(x-3)=x-23,解得:x=8或x=-7,故点C对应的数为-7或8;
BC,∴3AC=BC,∴3|x-3|=|23-x|,∴3(x-3)=23-x或3(x-3)=x-23,解得:x=8或x=-7,故点C对应的数为-7或8;
(3)若![]() 1=15,则x=28(舍)或x=﹣28;
1=15,则x=28(舍)或x=﹣28;
若x2-x+3=15,则x=-3(舍)或x=4;
综上,当输出M=15时,输入x的值为-28或4.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
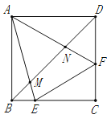
【题目】如图,正方形![]() 中,点
中,点![]() 分别在线段
分别在线段![]() 上运动,且满足
上运动,且满足![]() ,
,![]() 分别与
分别与![]() 相交于点
相交于点![]() ,下列说法中:①
,下列说法中:①![]() ;②点
;②点![]() 到线段
到线段![]() 的距离一定等于正方形的边长;③若
的距离一定等于正方形的边长;③若![]() ,则
,则![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() .其中结论正确的是___________;(将正确的序号填写在横线上)
.其中结论正确的是___________;(将正确的序号填写在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线交于点
的对角线交于点![]() ,把边
,把边![]() 、
、![]() 分别绕点
分别绕点![]() 、
、![]() 同时逆时针旋转
同时逆时针旋转![]() 得四边形
得四边形![]() ,其对角线交点为
,其对角线交点为![]() ,连接
,连接![]() .下列结论:
.下列结论:
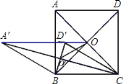
①四边形![]() 为菱形;
为菱形;
②![]() ;
;
③线段![]() 的长为
的长为![]() ;
;
④点![]() 运动到点
运动到点![]() 的路径是线段
的路径是线段![]() .其中正确的结论共有( )
.其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
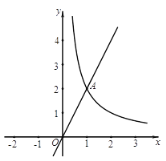
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于点A(1,2).
的图象交于点A(1,2).
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线l交于点B,与函数
与直线l交于点B,与函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点D.
轴交于点D.
①当点C是线段BD的中点时,求![]() 的值;
的值;
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
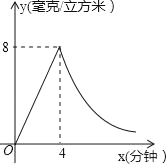
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2
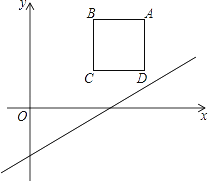
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com