
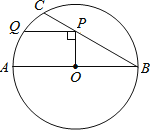
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图当PQ∥AB时,求PQ的长;
(2)当点P在BC上移动时,线段PQ长的最大值为______;此时,∠POQ的度数为______.
【答案】(1)![]() ;(2)
;(2)![]() ,60°
,60°
【解析】
连结OQ,如图1,由PQ∥AB,OP⊥PQ得到OP⊥AB,在Rt△OBP中,利用正切定义可计算出OP=3tan30°=![]() ,然后在Rt△OPQ中利用勾股定理可计算出PQ=
,然后在Rt△OPQ中利用勾股定理可计算出PQ=![]() ;
;
(2)连结OQ,如图2,在Rt△OPQ中,根据勾股定理得到PQ= PQ=![]() ,则当OP的长最小时,PQ的长最大,根据垂线段最短得到OP⊥BC,则OP=
,则当OP的长最小时,PQ的长最大,根据垂线段最短得到OP⊥BC,则OP=![]() OB=
OB=![]() ,所以PQ长的最大值=
,所以PQ长的最大值=![]()
解:(1)解:(1)连结OQ,如图1,
∵PQ∥AB,OP⊥PQ,
∴OP⊥AB,
在Rt△OBP中,∵tan∠B=![]() ,
,
∴OP=3tan30°=![]() ,
,
在Rt△OPQ中,∵OP=![]() ,OQ=3,
,OQ=3,
∴PQ=![]() =
=![]() ;
;
(2)连结OQ,如图2,
在Rt△OPQ中,PQ=![]() =
=![]() ,
,
当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=![]() OB=
OB=![]() ,
,
∴PQ长的最大值为![]() =
= ![]() ,
,
在Rt△QPO中,tan∠POQ=![]() =
=![]() =
=![]()
则∠POQ=60°,
故答案为:![]() ,60°.
,60°.


科目:初中数学 来源: 题型:
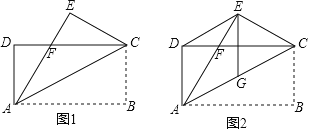
【题目】如图1,已知矩形ABCD,连接AC,将△ABC沿AC所在直线翻折,得到△AEC,AE交CD于点F.
(1)求证:DF=EF;
(2)如图2,若∠BAC=30°,点G是AC的中点,连接DE,EG,求证:四边形ADEG是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射手在一次射击中,射中![]() 环、
环、![]() 环、
环、![]() 环的概率分别是
环的概率分别是![]() 、
、![]() 、
、![]() ,那么,这个射手在这次射击中,射中
,那么,这个射手在这次射击中,射中![]() 环或
环或![]() 环的概率为________;不够
环的概率为________;不够![]() 环的概率为________.
环的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方形AOBC各顶点的坐标分别为A(0,3),O(0,0),B(3,0),C(3,3).若以原点为位似中心,将这个正方形的边长缩小为原来的![]() ,则新正方形的中心的坐标为_____.
,则新正方形的中心的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
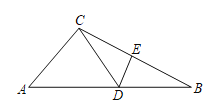
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE=2.
(1)若∠A=40°,求∠CDE;
(2)若图形中所有线段长均为整数,求CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
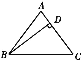
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,﹣3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则B′点的坐标为( )
A. (![]() , ﹣4) B. (
, ﹣4) B. (![]() , ﹣4) C. (
, ﹣4) C. (![]() , 4) D. (
, 4) D. (![]() , 4)
, 4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com