
分析 (1)根据“神秘数”的定义,只需看能否把28和2012这两个数写成两个连续偶数的平方差即可判断;
(2)运用平方差公式进行计算,进而判断即可;
(3)运用平方差公式进行计算,进而判断即可.
解答 解:(1)∵28=82-62,2012=5042-5022,
∴28是“神秘数”;2012是“神秘数”;
(2)两个连续偶数构成的“神秘数”是4的倍数.理由如下:
(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∴两个连续偶数构成的“神秘数”是4的倍数,
∵2k+1是奇数,
∴它是4的倍数,不是8的倍数;
(3)设两个连续的奇数为:2k+1,2k-1,则
(2k+1)2-(2k-1)2=8k,
此数是8的倍数,而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
点评 此题主要考查了平方差公式的应用,此题是一道新定义题目,熟练记忆平方差公式是解题关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
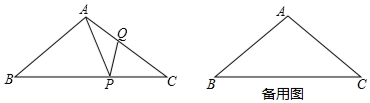
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
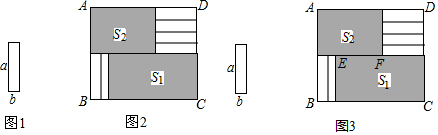
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
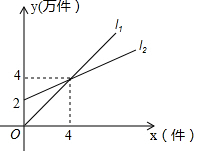 如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)
如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com