
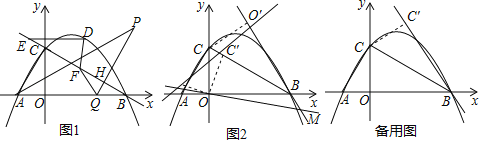
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏ![]() ”κy÷αΫΜ”ΎΒψCΘ§”κx÷αΫΜ”ΎΒψAΓΔBΘ®ΒψA‘ΎΒψBΉσ±ΏΘ©Θ§OΈΣΉχ±ξ‘≠ΒψΘ°ΒψD «÷±œΏBC…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψDΉςDEΓΈx÷αΫΜ÷±œΏBC”ΎΒψEΘ°ΒψPΈΣΓœCABΫ«ΤΫΖ÷œΏ…œΒΡ“ΜΕ·ΒψΘ§ΙΐΒψPΉςPQΓΆBC”ΎΒψHΘ§ΫΜx÷α”ΎΒψQΘΜΒψF «÷±œΏBC…œΒΡ“ΜΗωΕ·ΒψΘ°
”κy÷αΫΜ”ΎΒψCΘ§”κx÷αΫΜ”ΎΒψAΓΔBΘ®ΒψA‘ΎΒψBΉσ±ΏΘ©Θ§OΈΣΉχ±ξ‘≠ΒψΘ°ΒψD «÷±œΏBC…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψDΉςDEΓΈx÷αΫΜ÷±œΏBC”ΎΒψEΘ°ΒψPΈΣΓœCABΫ«ΤΫΖ÷œΏ…œΒΡ“ΜΕ·ΒψΘ§ΙΐΒψPΉςPQΓΆBC”ΎΒψHΘ§ΫΜx÷α”ΎΒψQΘΜΒψF «÷±œΏBC…œΒΡ“ΜΗωΕ·ΒψΘ°
Θ®1Θ©Β±œΏΕΈDEΒΡ≥ΛΕ»Ήν¥σ ±Θ§«σDF+FQ+![]() PQΒΡΉν–Γ÷ΒΘ°
PQΒΡΉν–Γ÷ΒΘ°
Θ®2Θ©»γΆΦ2Θ§ΫΪΓςBOC―ΊBC±ΏΥυ‘Ύ÷±œΏΖ≠’έΘ§ΒΟΒΫΓςBOCΓδΘ§ΒψMΈΣ÷±œΏBOΓδ…œ“ΜΕ·ΒψΘ§ΫΪΓςAOC»ΤΒψOΥ≥ ±’κ–ΐΉΣΠΝΕ»Θ®0ΓψΘΦΠΝΘΦ180ΓψΘ©ΒΟΒΫΓςAΓδOCΓδΘ§Β±÷±œΏAΓδCΓδΘ§÷±œΏBOΓδΘ§÷±œΏOMΈß≥…ΒΡΆΦ–Έ «Β»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ωΗΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡΟφΜΐΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©Έß≥…ΒΡ»ΐΫ«–ΈΟφΜΐΈΣΘΚ
ΘΜΘ®2Θ©Έß≥…ΒΡ»ΐΫ«–ΈΟφΜΐΈΣΘΚ![]()
![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
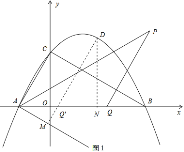
Θ®1Θ©«σ≥ωΒψAΓΔBΓΔCΒΡΉχ±ξΒΟAC≥ΛΕ»”κ÷±œΏBCΫβΈω ΫΘ§…ηDΘ®aΘ§![]() Θ©Θ§÷ΣEΘ®
Θ©Θ§÷ΣEΘ®![]() Θ©ΓΔDEΘΫa©¹
Θ©ΓΔDEΘΫa©¹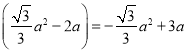 Θ§»ΜΚσ«σ≥ωaΤδΉν¥σ÷ΒΘ§Φ¥Ω…«σ≥ωDEΒΡΉν¥σ÷ΒΘ§¥Υ ±Ω…«σ≥ωDΒΡΉχ±ξΘ°‘Ό÷ΛAQΘΫPQΘ§ΒΟ
Θ§»ΜΚσ«σ≥ωaΤδΉν¥σ÷ΒΘ§Φ¥Ω…«σ≥ωDEΒΡΉν¥σ÷ΒΘ§¥Υ ±Ω…«σ≥ωDΒΡΉχ±ξΘ°‘Ό÷ΛAQΘΫPQΘ§ΒΟ![]() ΘΫ
ΘΫ![]() Θ§ΫΪ…δœΏAB»ΤAΥ≥ ±’κ–ΐΉΣ30ΓψΒΟΒΫ÷±œΏAMΘ§ΙΐΒψDΉςAMΒΡ¥ΙœΏ”ΎΒψMΘ§ΫΜx÷α”ΎΒψQΓδΘ§‘ρ
Θ§ΫΪ…δœΏAB»ΤAΥ≥ ±’κ–ΐΉΣ30ΓψΒΟΒΫ÷±œΏAMΘ§ΙΐΒψDΉςAMΒΡ¥ΙœΏ”ΎΒψMΘ§ΫΜx÷α”ΎΒψQΓδΘ§‘ρ![]() Θ°Β±Q‘ΥΕ·ΒΫQΓδ ±Θ§”–
Θ°Β±Q‘ΥΕ·ΒΫQΓδ ±Θ§”–![]() ΘΫDMΘ§ΙΐDΉςDNΓΆx÷α”ΎΒψNΘ§Ω…ΒΟΓςAQΓδM”κΓςDQΓδNœύΥΤΘ§»ΜΚσ«σ≥ωΗςΗωœΏΕΈΒΡ≥ΛΦ¥Ω…ΘΜ
ΘΫDMΘ§ΙΐDΉςDNΓΆx÷α”ΎΒψNΘ§Ω…ΒΟΓςAQΓδM”κΓςDQΓδNœύΥΤΘ§»ΜΚσ«σ≥ωΗςΗωœΏΕΈΒΡ≥ΛΦ¥Ω…ΘΜ
Θ®2Θ©Ζ÷Νυ÷÷«ιΩωΫχ––Χ÷¬έΘ§»ΜΚσ«σ≥ωΟΩ“Μ÷÷«ιΩωœ¬άϊ”Ο«–œΏΒΡ–‘÷ ΓΔ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ―ϋ≥ΛΘ§άϊ”Ο÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ¥πΑΗΘ°
Θ®1Θ©»γΆΦ1Θ§
Β±xΘΫ0 ±Θ§yΘΫ3Θ°
Β±yΘΫ0 ±Θ§![]() Θ°
Θ°
Γύ![]() Θ§
Θ§![]() Θ§
Θ§![]()
ΓύACΓΆBCΘ§«“ΓœABCΘΫ30ΓψΘ§ACΘΫ![]() Θ§«“
Θ§«“![]()
…ηDΘ®aΘ§![]() Θ©Θ§‘ρEΘ®
Θ©Θ§‘ρEΘ®![]() Θ©
Θ©
ΓύDEΘΫa©¹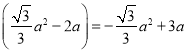
ΓύΒ±aΘΫ©¹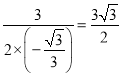 ±Θ§DEΉν¥σΘ°¥Υ ±DΘ®
±Θ§DEΉν¥σΘ°¥Υ ±DΘ®![]() Θ©
Θ©
ΓΏAPΤΫΖ÷ΓœCABΘ§
ΓύΓœPABΘΫ![]() ΓœCABΘΫ30ΓψΘ§
ΓœCABΘΫ30ΓψΘ§
ÿPQâBCȧ
ΓύΓœPQBΘΫ60ΓψΘ§
ΓύΓœPΘΫΓœPQB©¹ΓœPABΘΫ60Γψ©¹30ΓψΘΫ30ΓψΘΫΓœPABΘ§
ÿPQâBCȧ
ΓύPQBΘΫ60ΓψΘ§
ΓύAQΘΫPQΘ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΫΪ…δœΏAB»ΤAΥ≥ ±’κ–ΐΉΣ30ΓψΒΟΒΫ÷±œΏAMΘ§ΙΐΒψDΉςAMΒΡ¥ΙœΏ”ΎΒψMΘ§ΫΜx÷α”ΎΒψQΓδΘ§‘ρ![]() Θ°
Θ°
Β±Q‘ΥΕ·ΒΫQΓδ ±Θ§”–![]() ΘΫDMΘ§
ΘΫDMΘ§
ΙΐDΉςDNΓΆx÷α”ΎΒψNΘ§Ω…ΒΟΓςAQΓδM”κΓςDQΓδNœύΥΤΘ§
DNΘΫDyΘΫ![]() Θ§ANΘΫ
Θ§ANΘΫ![]()
ΓύQΓδNΘΫ![]() Θ§DQΓδΘΫ
Θ§DQΓδΘΫ![]() Θ§AQΓδΘΫAN©¹QΓδNΘΫ
Θ§AQΓδΘΫAN©¹QΓδNΘΫ![]()
ΓύQΓδMΘΫ![]() Θ§
Θ§
ΓύDMΘΫDQΓδ+QΓδMΘΫ![]()
![]() ΘΫDMΘΫ
ΘΫDMΘΫ![]() Θ°
Θ°
Θ®2Θ©ΒΎ“Μ÷÷«ιΩωΘΚ»γΆΦ2Θ§
NHΘΫrΘΫ![]() Θ§QHΘΫ
Θ§QHΘΫ![]() ΘΫ
ΘΫ![]() Θ§OQΘΫ2rΘΫ3Θ§
Θ§OQΘΫ2rΘΫ3Θ§
QNΘΫQH©¹NHΘΫ![]() Θ§QBΘΫ3
Θ§QBΘΫ3![]() Θ§QPΘΫ
Θ§QPΘΫ![]() Θ§
Θ§
PNΘΫPQ©¹QNΘΫ6Θ§S1ΘΫ18Θ°
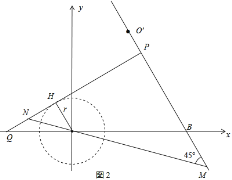
ΒΎΕΰ÷÷«ιΩωΘ§»γΆΦ3Θ§
QHΘΫ![]() Θ§HNΘΫrΘΫ
Θ§HNΘΫrΘΫ![]() Θ§
Θ§
QBΘΫ3+3![]() Θ§QPΘΫ
Θ§QPΘΫ![]() Θ§
Θ§
PNΘΫPQ©¹QH©¹HNΘΫ3Θ§![]() ΘΜ
ΘΜ
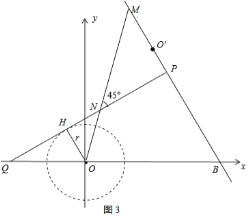
ΒΎ»ΐ÷÷«ιΩωΘ§»γΆΦ4Θ§
ONΘΫ![]() Θ§OMΘΫ
Θ§OMΘΫ![]() Θ§
Θ§
MQΘΫOM©¹rΘΫ![]() Θ§
Θ§
![]()
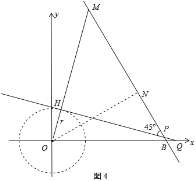
ΒΎΥΡ÷÷«ιΩωΘ§»γΆΦ5Θ§
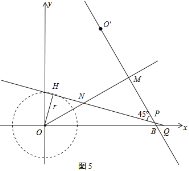
OBΘΫ![]() Θ§OMΘΫ
Θ§OMΘΫ![]() Θ§ONΘΫ
Θ§ONΘΫ![]() Θ§MNΘΫOM©¹0NΘΫ
Θ§MNΘΫOM©¹0NΘΫ![]() Θ§
Θ§
![]() Θ°
Θ°
ΒΎΈε÷÷«ιΩωΘ§»γΆΦ6Θ§
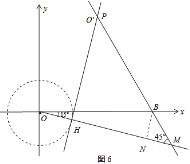
MNΘΫBNΘΫOBsin15ΓψΘΫ![]()
ONΘΫOBcos15ΓψΘΫ![]() Θ§
Θ§
OMΘΫON+MNΘΫ![]() Θ§HMΘΫOM©¹rΘΫ
Θ§HMΘΫOM©¹rΘΫ![]() Θ§
Θ§
![]() ΘΜ
ΘΜ
ΒΎΝυ÷÷«ιΩωΘ§»γΆΦ7Θ§
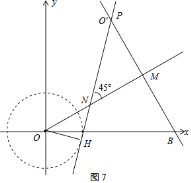
OMΘΫ![]() Θ§ONΘΫ
Θ§ONΘΫ![]() Θ§MNΘΫOM©¹ONΘΫ
Θ§MNΘΫOM©¹ONΘΫ![]() Θ§
Θ§
![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§Έß≥…ΒΡ»ΐΫ«–ΈΟφΜΐΈΣΘΚ![]() ΘΜ
ΘΜ![]() Θ°
Θ°


 ΑΌ«ΩΟϊ–ΘΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
ΑΌ«ΩΟϊ–ΘΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ ΚΟ≥…Φ®1Φ”1ΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
ΚΟ≥…Φ®1Φ”1ΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ Ϋ𹥑ΣΦ®”≈ΚΟΨμœΒΝ–¥πΑΗ
Ϋ𹥑ΣΦ®”≈ΚΟΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΟς¥σ―ß±œ“ΒΜΊΦ“œγ¥¥“ΒΘ§ΒΎ“ΜΤΎ≈ύ÷≤≈ηΨΑ”κΜ®ΜήΗς50≈η έΚσΆ≥ΦΤΘ§≈ηΨΑΒΡΤΫΨυΟΩ≈ηάϊ»σ «160‘ΣΘ§Μ®ΜήΒΡΤΫΨυΟΩ≈ηάϊ»σ «19‘ΣΘ§Βς―–ΖΔœ÷ΘΚ
ΔΌ≈ηΨΑΟΩ‘ωΦ”1≈ηΘ§≈ηΨΑΒΡΤΫΨυΟΩ≈ηάϊ»σΦθ…Ό2‘Σ;ΟΩΦθ…Ό1≈ηΘ§≈ηΨΑΒΡΤΫΨυΟΩ≈ηάϊ»σ‘ωΦ”2‘Σ;ΔΎΜ®ΜήΒΡΤΫΨυΟΩ≈ηάϊ»σ Φ÷’≤Μ±δ.
–ΓΟςΦΤΜ°ΒΎΕΰΤΎ≈ύ÷≤≈ηΨΑ”κΜ®ΜήΙ≤100≈ηΘ§…η≈ύ÷≤ΒΡ≈ηΨΑ±»ΒΎ“ΜΤΎ‘ωΦ”x≈ηΘ§ΒΎΕΰΤΎ≈ηΨΑ”κΜ®Μή έΆξΚσΒΡάϊ»σΖ÷±πΈΣW1Θ§W2Θ®ΒΞΈΜΘΚ‘ΣΘ©
Θ®1Θ©”ΟΚ§xΒΡ¥ζ ΐ ΫΖ÷±π±μ ΨW1Θ§W2;
Θ®2Θ©Β±x»ΓΚΈ÷Β ±Θ§ΒΎΕΰΤΎ≈ύ÷≤ΒΡ≈ηΨΑ”κΜ®Μή έΆξΚσΜώΒΟΒΡΉήάϊ»σWΉν¥σΘ§Ήν¥σΉήάϊ»σ «Εύ…Ό?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓ―O÷–Θ§ACΈΣ÷±ΨΕΘ§MAΓΔMBΖ÷±π«–Γ―O”ΎΒψAΓΔBΘ°
Θ®ΔώΘ©»γΆΦΔΌΘ§»τΓœBAC=250Θ§«σΓœAMBΒΡ¥σ–ΓΘΜ
Θ®ΔρΘ©»γΆΦΔΎΘ§ΙΐΒψBΉςBDΓΆAC”ΎΒψEΘ§ΫΜΓ―O”ΎΒψDΘ§»τBD=MAΘ§«σΓœAMBΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
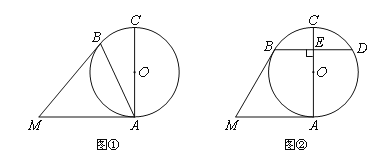
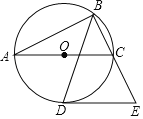
ΓΨΧβΡΩΓΩ»γΆΦΘ§“‘ΓςABCΒΡ±ΏACΈΣ÷±ΨΕΒΡO«ΓΈΣΓςABCΒΡΆβΫ”‘≤Θ§ΓœABCΒΡΤΫΖ÷œΏΫΜO”ΎΒψDΘ§ΙΐΒψDΉςDEΓΈACΫΜBCΒΡ―”≥ΛœΏ”ΎΒψE
Θ®1Θ©«σ÷ΛΘΚDE «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τABΘΫ4![]() Θ§BCΘΫ2
Θ§BCΘΫ2![]() Θ§«σDEΒΡ≥ΛΘ°
Θ§«σDEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
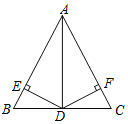
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ABΘΫACΘ§ΒψDΈΣ±ΏBC…œ“ΜΒψΘ§«“ADΤΫΖ÷ΓœBACΘ§DEΓΆAB”ΎΒψEΘ§DFΓΆAC”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚBEΘΫCFΘΜ
Θ®2Θ©»τΓœBΘΫ40ΓψΘ§«σΓœADFΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΑΥΡξΦΕ“ΜΑύΩΣ’ΙΝΥΓΑΕΝ“Μ±ΨΚΟ ιΓ±ΒΡΜνΕ·Θ§ΑύΈ·ΜαΕ‘―ß…ζ‘ΡΕΝ ιΦ°ΒΡ«ιΩωΫχ––ΝΥΈ ΨμΒς≤ιΘ§Έ Ψμ…η÷ΟΝΥΓΑ–ΓΥΒΓ±ΓΔΓΑœΖΨγΓ±ΓΔΓΑ…ΔΈΡΓ±ΓΔΓΑΤδΥϊΓ±ΥΡΗωάύ±πΘ§ΟΩΈΜΆ§―ßΫω―Γ“ΜœνΘ§ΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ±μΚΆ…»–ΈΆ≥ΦΤΆΦΘ°ΗυΨίΆΦ±μΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
άύ±π | ΤΒ ΐΘ®»Υ ΐΘ© | ΤΒ¬ |
–ΓΥΒ | 0.5 | |
œΖΨγ | 4 | |
…ΔΈΡ | 10 | 0.25 |
ΤδΥϊ | 6 | |
ΚœΦΤ | m | 1 |
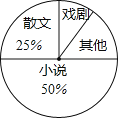
Θ®1Θ©ΦΤΥψmΘΫΓΓ ΓΓΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§ΓΑΤδΥϊΓ±άύΥυ’ΦΒΡΑΌΖ÷±»ΈΣΓΓ ΘΜ
Θ®3Θ©‘ΎΒς≤ιΈ Ψμ÷–Θ§ΦΉΓΔ““ΓΔ±ϊΓΔΕΓΥΡΈΜΆ§―ß―Γ‘ώΝΥΓΑœΖΨγΓ±άύΘ§œ÷¥”÷–»Έ“β―Γ≥ω2ΟϊΆ§―ß≤ΈΦ”―ß–ΘΒΡœΖΨγ…γΆ≈Θ§«κ”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®Θ§«σ―Γ»ΓΒΡ2»Υ«ΓΚΟ «““ΚΆ±ϊΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
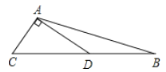
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΒψD «BCΒΡ÷–ΒψΘ§DAΓΆACΘ§tanΓœBAD=![]() Θ§AB=
Θ§AB=![]() Θ§‘ρBCΒΡ≥ΛΕ»ΈΣ______Θ°
Θ§‘ρBCΒΡ≥ΛΕ»ΈΣ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΥ“‘ΎΡœ±±ΚΫœΏ…œΒΡ≤βΝΩ¥§Θ§”ΎAΒψ¥Π≤βΒΟΚΘΒΚB‘ΎΒψAΒΡΡœΤΪΕΪ30ΓψΖΫœρΘ§ΦΧ–χœρΡœΚΫ––30ΚΘάοΒΫ¥οCΒψ ±Θ§≤βΒΟΚΘΒΚB‘ΎCΒψΒΡ±±ΤΪΕΪ15ΓψΖΫœρΘ§Ρ«Ο¥ΚΘΒΚBάκ¥ΥΚΫœΏΒΡΉνΫϋΨύάκ «Θ®ΫαΙϊ±ΘΝτ–Γ ΐΒψΚσΝΫΈΜΘ©Θ®≤ΈΩΦ ΐΨίΘΚ![]() Θ©Θ® Θ©
Θ©Θ® Θ©
A. 4.64ΚΘάο B. 5.49ΚΘάο C. 6.12ΚΘάο D. 6.21ΚΘάο
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎABCD÷–Θ§AEΘ§CFΖ÷±π «ΓœBADΚΆΓœBCDΒΡΤΫΖ÷œΏΘ§ΧμΦ”“ΜΗωΧθΦΰΘ§»‘ΈόΖ®≈–ΕœΥΡ±Ώ–ΈAECFΈΣΝβ–ΈΒΡ «Θ® Θ©

A. AE=AFB. EFΓΆACC. ΓœB=60ΓψD. AC «ΓœEAFΒΡΤΫΖ÷œΏ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com