
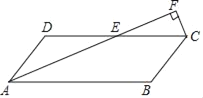
【题目】如图,四边形ABCD为平行四边形,AD=1,AB=3,∠DAB=60°,点E为边CD上一动点,过点C作AE的垂线交AE的延长线于点F.
(1)求∠D的度数;
(2)若点E为CD的中点,求EF的值;
(3)当点E在线段CD上运动时,![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
【答案】(1)∠ADC=120°;(2)EF=![]() ,(3)有最大值,最大值为:
,(3)有最大值,最大值为:![]()
【解析】
(1)由四边形ABCD是平行四边形,得AB∥CB,进而即可得到答案;
(2)作AH⊥CD交CD的延长线于H,由在Rt△ADH中,∠H=90°,∠ADH=60°,得A=![]() ,DH=
,DH=![]() ,结合勾股定理得AE=
,结合勾股定理得AE=![]() ,易证△AEH∽△CEF,得
,易证△AEH∽△CEF,得![]() ,进而即可求解;
,进而即可求解;
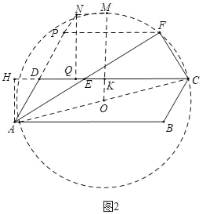
(3)作△AFC的外接圆⊙O,作AH⊥CD交CD的延长线于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于N,作NQ⊥CD于Q.易得PA的值最大时,![]() 的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=
的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=![]() ,从而得AN=AD+DN=
,从而得AN=AD+DN=![]() ,进而即可得到答案.
,进而即可得到答案.
(1)∵四边形ABCD是平行四边形,
∴AB∥CB,
∴∠ADC+∠DAB=180°,
∵∠DAB=60°,
∴∠ADC=120°.
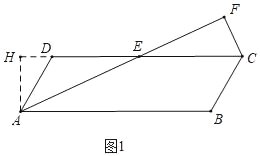
(2)作AH⊥CD交CD的延长线于H,如图1,
∵在Rt△ADH中,∠H=90°,∠ADH=60°,AD=2,
∴AH=ADsin60°=![]() ,DH=ADcos60°=
,DH=ADcos60°=![]() ,
,
∵DE=EC=![]() ,
,
∴EH=DH+DE=2,
∴AE=![]() ,
,
∵CF⊥AF,
∴∠F=∠H=90°,
∵∠AEH=∠CEF,
∴△AEH∽△CEF,
∴![]() ,
,
∴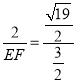 ,
,
∴EF=![]() .
.
∵DE∥PF,
∴![]() ,
,
∵AD是定值,
∴PA的值最大时,![]() 的值最大,
的值最大,
观察图形可知,当点F与点M重合时,PA的值最大,最大值=AN的长,
由(2)可知,AH=![]() ,CH=
,CH=![]() ,∠H=90°,
,∠H=90°,
∴AC=![]() ,
,
∴OM=![]() AC=
AC=![]() ,
,
∵OK∥AH,AO=OC,
∴KH=KC,
∴OK=![]() =
=![]() ,
,
∴MK=NQ=![]() ﹣
﹣![]() ,
,
在Rt△NDQ中,DN=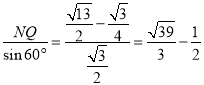 ,
,
∴AN=AD+DN=![]() ,
,
∴![]() 的最大值=
的最大值=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
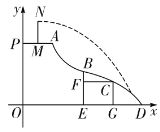
【题目】游乐园新建的一种新型水上滑道如图,其中线段![]() 表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道
表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道![]() 可以看作反比例函数图象的一部分,滑道
可以看作反比例函数图象的一部分,滑道![]() 可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数
可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数![]() 的顶点,且点B到水面的距离
的顶点,且点B到水面的距离![]() ,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离
,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离![]() ,与点B的水平距离
,与点B的水平距离![]() .
.
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道![]() 的水平距离;
的水平距离;
(3)若小明站在平台上相距y轴![]() 的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台
的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台![]() ,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道
,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道![]() 上(包括B、D两点),直接写出p的取值范围.
上(包括B、D两点),直接写出p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
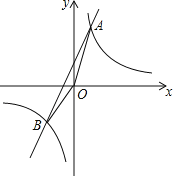
(1)求△AOB的面积;
(2)结合图象直接写出y1<y2时x的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,他们的形状、大小、质地等完全相同.小兰先从盒子里随机取出一个小球,记下数字为x,放回盒子,摇匀后,再由小田随机取出一个小球,记下数字为y
(1)用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
(2)求小兰、小田各取一次小球所确定的点(x,y)落在反比例函数![]() 的图象上的频率;
的图象上的频率;
(3)求小兰、小田各取一次小球所确定的数x,y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
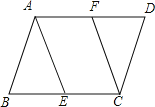
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两所学校的学生都参加了某次体育测试,成绩均为7﹣10分,且为整数.亮亮分别从这两所学校各随机抽取一部分学生的测试成绩,共200份,并绘制了如下尚不完整的统计图.
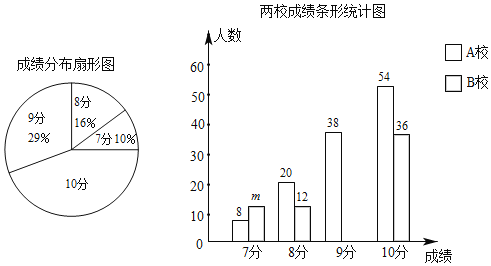
(1)这200份测试成绩的中位数是 分,m= ;
(2)补全条形统计图;扇形统计图中,求成绩为10分所在扇形的圆心角的度数.
(3)亮亮算出了“1名A校学生的成绩被抽到”的概率是![]() ,请你估计A校成绩为8分的学生大约有多少名.
,请你估计A校成绩为8分的学生大约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.

(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com