
ЁОЬтФПЁПдкбЇаЃПЊеЙЕФЁАЯзАЎаФЁБЛюЖЏжаЃЌаЁЖЋЭЌбЇДђЫудкЪюМйЦкМфАяжњвЛМвЩчЛсИЃРћЪщЕъЭЦЯњAЁЂBЁЂCЁЂDЫФжжЪщПЏЃЎЮЊСЫСЫНтЫФжжЪщПЏЕФЯњЪлЧщПіЃЌаЁЖЋЖдЮхдТЗнетЫФжжЪщПЏЕФЯњЪлСПНјааСЫЭГМЦЃЌаЁЖЋЭЈЙ§ВЩМЏЪ§ОнЃЌЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМБэЃЈШчЭМЃЉЃЌЧыФуИљОнЫљИјГіЕФаХЯЂНтД№вдЯТЮЪЬтЃК
ЪщПЏжжРр | ЦЕЪ§ | ЦЕТЪ |
A | ЁЁ ЁЁ | 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 | ЁЁ ЁЁ |
ЃЈ1ЃЉЬюГфЦЕТЪЗжВМБэжаЕФПеИёМАВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉШєИУЪщЕъМЦЛЎЖЈЙКДЫЫФжжЪщПЏ6000ВсЃЌЧыФуМЦЫуBжжЪщПЏгІВЩЙКЖрЩйВсНЯКЯЪЪЃП
ЃЈ3ЃЉеыЖдЕїВщНсЙћЃЌЧыФуАяжњаЁЖЋЭЌбЇИјИУЪщЕъЬсвЛЬѕКЯРэЛЏЕФНЈвщЃЎ
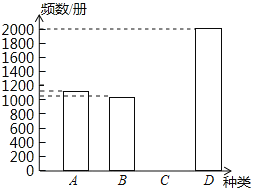
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉBжжЪщПЏгІВЩЙК1200ВсНЯКЯЪЪЃЛЃЈ3ЃЉдкЙКЪщЪБгІИУЖрЙКТђDРрЪщПЏЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЭГМЦБэКЭжБЗНЭМПЩжЊЃКDРрЪщПЏЕФЦЕТЪЮЊ1-0.25-0.20-0.15=0.40ЃЛAРрЪщПЏЕФЦЕЪ§ЮЊ1250ЃЛ
ЃЈ2ЃЉМЦЛЎЖЈЙКДЫЫФжжЪщПЏ6000ВсЃЌдђBжжЪщПЏгІВЩЙК6000ЁС0.20=1200ВсЃЛ
ЃЈ3ЃЉдкЙКЪщЪБгІИУЖрЙКТђDРрЪщПЏЃЈжЛвЊКЯРэМДПЩЃЉЃЎ
НтЃКЃЈ1ЃЉЭъГЩБэИёКЭжБЗНЭМШчЯТЭМЃК
ЪщПЏжжРр | ЦЕЪ§ | ЦЕТЪ |
A | 1250 | 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 | 0.4 |
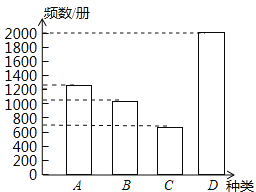
ЃЈ2ЃЉ6000ЁС0.2ЃН1200ЃЈВсЃЉЃЛ
Д№ЃКBжжЪщПЏгІВЩЙК1200ВсНЯКЯЪЪЃЛ
ЃЈ3ЃЉдкЙКЪщЪБгІИУЖрЙКТђDРрЪщПЏЃЎ


 ЕЅдЊМгЦкФЉИДЯАЯШЗцДѓПМОэЯЕСаД№АИ
ЕЅдЊМгЦкФЉИДЯАЯШЗцДѓПМОэЯЕСаД№АИ ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМйЩшФГЩЬГЁЕиЯТЭЃГЕГЁга5ИіГіШыПкЃЌУПЬьдчГП7ЕуПЊЪМЖдЭтЭЃГЕЧвДЫЪБГЕЮЛПежУТЪЮЊ90%ЃЌдкУПИіГіШыПкЕФГЕСОЪ§ОљЪЧдШЫйГіШыЕФЧщПіЯТЃЌШчЙћПЊЗХ2ИіНјПкКЭ3ИіГіПкЃЌ6аЁЪБГЕПтЧЁКУЭЃТњЃЛШчЙћПЊЗХ3ИіНјПкКЭ2ИіГіПкЃЌ3аЁЪБГЕПтЧЁКУЭЃТњЃЎ2019ФъЧхУїНкЦкМфЃЌгЩгкЩЬГЁШЫЪ§діЖрЃЌдчГП7ЕуЪБЕФГЕЮЛПежУТЪБфЮЊ60%ЃЌвђЮЊГЕПтИФдьЃЌжЛФмПЊЗХ1ИіНјПкКЭ1ИіГіПкЃЌдђДгдчГП7ЕуПЊЪМОЙ§______аЁЪБГЕПтЧЁКУЭЃТњЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ОЙ§
ОЙ§![]() ЃЌ
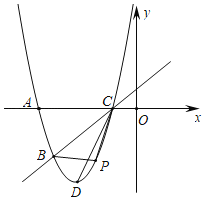
ЃЌ![]() СНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌЖЅЕуЮЊDЃЌСЌНсCDЃЎ
СНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌЖЅЕуЮЊDЃЌСЌНсCDЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊИУХзЮяЯпЩЯвЛЖЏЕуЃЈгыЕуBЁЂCВЛжиКЯЃЉЃЌЩшЕуPЕФКсзјБъЮЊtЃЎ
ЂйЕБЕуPдкжБЯпBCЕФЯТЗНдЫЖЏЪБЃЌЧѓ![]() ЕФУцЛ§ЕФзюДѓжЕЃЛ
ЕФУцЛ§ЕФзюДѓжЕЃЛ
ЂкИУХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУ![]() ШєДцдкЃЌЧѓГіЫљгаЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ШєДцдкЃЌЧѓГіЫљгаЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§y=![]() (kЃО0ЃЌxЃО0)ЕФЭМЯѓгыЕШБпШ§НЧаЮOABЕФБпOAЃЌABЗжБ№НЛгкЕуMЃЌNЃЌЧвOM=2MAЃЌШєAB=3ЃЌФЧУДЕуNЕФКсзјБъЮЊ(ЁЁЁЁ)
(kЃО0ЃЌxЃО0)ЕФЭМЯѓгыЕШБпШ§НЧаЮOABЕФБпOAЃЌABЗжБ№НЛгкЕуMЃЌNЃЌЧвOM=2MAЃЌШєAB=3ЃЌФЧУДЕуNЕФКсзјБъЮЊ(ЁЁЁЁ)
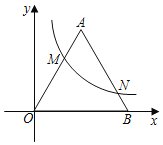
A.![]() B.
B.![]() C.4D.6
C.4D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЫљЪОЃЌвбжЊе§ЗНаЮABCDКЭе§ЗНаЮAEFGЃЌСЌНгDGЃЌBEЃЎ
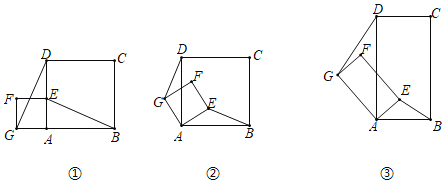
ЃЈ1ЃЉЗЂЯжЃКЕБе§ЗНаЮAEFGШЦЕуAа§зЊЃЌШчЭМЂкЫљЪОЃЎ
ЂйЯпЖЮDGгыBEжЎМфЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЛ
ЂкжБЯпDGгыжБЯпBEжЎМфЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЬНОПЃКШчЭМЂлЫљЪОЃЌШєЫФБпаЮABCDгыЫФБпаЮAEFGЖМЮЊОиаЮЃЌЧвADЃН2ABЃЌAGЃН2AEЪБЃЌЩЯЪіНсТлЪЧЗёГЩСЂЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉгІгУЃКдкЃЈ2ЃЉЕФЧщПіЯТЃЌСЌНгBGЁЂDEЃЌШєAEЃН1ЃЌABЃН2ЃЌЧѓBG2+DE2ЕФжЕЃЈжБНгаДГіНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
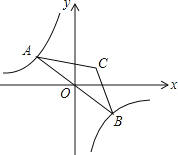
ЁОЬтФПЁПШчЭМЃЌвбжЊЗДБШР§КЏЪ§yЃНЉ![]() ЕФЭМЯѓгыжБЯпyЃНkxЃЈkЃМ0ЃЉЯрНЛгкЕуAЁЂBЃЌвдABЮЊЕззїЕШбќШ§НЧаЮЃЌЪЙЁЯACBЃН120ЁуЃЌЧвЕуCЕФЮЛжУЫцзХkЕФВЛЭЌШЁжЕЖјЗЂЩњБфЛЏЃЌЕЋЕуCЪМжедкФГвЛКЏЪ§ЭМЯѓЩЯЃЌдђетИіЭМЯѓЫљЖдгІЕФКЏЪ§НтЮіЪНЮЊ__ЃЎ
ЕФЭМЯѓгыжБЯпyЃНkxЃЈkЃМ0ЃЉЯрНЛгкЕуAЁЂBЃЌвдABЮЊЕззїЕШбќШ§НЧаЮЃЌЪЙЁЯACBЃН120ЁуЃЌЧвЕуCЕФЮЛжУЫцзХkЕФВЛЭЌШЁжЕЖјЗЂЩњБфЛЏЃЌЕЋЕуCЪМжедкФГвЛКЏЪ§ЭМЯѓЩЯЃЌдђетИіЭМЯѓЫљЖдгІЕФКЏЪ§НтЮіЪНЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИљЮЊСэвЛИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЌвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉ
гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИљЮЊСэвЛИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЌвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉ
A.ЗНГЬ![]() ЪЧБЖИљЗНГЬЃЛ
ЪЧБЖИљЗНГЬЃЛ
B.Шє![]() ЪЧБЖИљЗНГЬЃЌдђ
ЪЧБЖИљЗНГЬЃЌдђ![]() ЃЛ
ЃЛ
C.ШєЗНГЬ![]() ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу
ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу![]() ЖМдкХзЮяЯп
ЖМдкХзЮяЯп![]() ЩЯЃЌдђЗНГЬ
ЩЯЃЌдђЗНГЬ![]() ЕФвЛИіИљЮЊ
ЕФвЛИіИљЮЊ![]() ЃЛ
ЃЛ
D.ШєЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌдђЙигк
ЕФЭМЯѓЩЯЃЌдђЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЪЧБЖИљЗНГЬЃЎ
ЪЧБЖИљЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
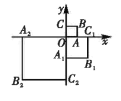
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌе§ЗНаЮ
жаЃЌе§ЗНаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЗжБ№дк
ЗжБ№дк![]() ЃЌ
ЃЌ![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЃЎНЋе§ЗНаЮ
ЃЎНЋе§ЗНаЮ![]() ШЦдЕу
ШЦдЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕУЕНе§ЗНаЮ
ЃЌЕУЕНе§ЗНаЮ![]() ЃЌдйНЋе§ЗН
ЃЌдйНЋе§ЗН![]() ШЦдЕу
ШЦдЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕУЕНе§ЗНаЮ
ЃЌЕУЕНе§ЗНаЮ![]() ЃЌвдДЫЙцТЩЃЌЕУЕНе§ЗНаЮ
ЃЌвдДЫЙцТЩЃЌЕУЕНе§ЗНаЮ![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ__________ЃЎ
ЕФзјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌОЙ§Еу
зѓВрЃЉЃЌОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() ЃК
ЃК![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊ
ЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
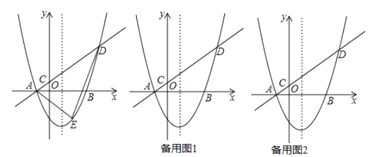
ЃЈ1ЃЉжБНгаДГіЕу![]() ЕФзјБъЃЌВЂгУКЌ
ЕФзјБъЃЌВЂгУКЌ![]() ЕФЪНзгБэЪОжБЯп
ЕФЪНзгБэЪОжБЯп![]() ЕФКЏЪ§БэДяЪНЃЈЦфжа
ЕФКЏЪ§БэДяЪНЃЈЦфжа![]() ЁЂ
ЁЂ![]() гУКЌ
гУКЌ![]() ЕФЪНзгБэЪОЃЉЃЎ
ЕФЪНзгБэЪОЃЉЃЎ
ЃЈ2ЃЉЕу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЯТЗНХзЮяЯпЩЯвЛЕуЃЌЕБ
ЯТЗНХзЮяЯпЩЯвЛЕуЃЌЕБ![]() ЕФУцЛ§ЕФзюДѓжЕЮЊ
ЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЪБЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЪБЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉЩшЕу![]() ЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌЕу
ЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌЕу![]() дкХзЮяЯпЩЯЃЌвдЕу
дкХзЮяЯпЩЯЃЌвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊОиаЮЃПШєФмЃЌЧѓГіЕу
ЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊОиаЮЃПШєФмЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com