
ЁОЬтФПЁПвбжЊЃКШчЭМ.дкЁїABCжа.AB=AC=5cmЃЌBC=6cm.ЕуPгЩBГіЗЂЃЌбиBCЗНЯђдШЫйдЫЖЏ.ЫйЖШЮЊ1cm/s.ЭЌЪБЃЌЕуQДгЕуAГіЗЂЃЌбиACЗНЯђдШЫйдЫЖЏ.ЫйЖШЮЊ1cm/sЃЌЙ§ЕуPзїPM![]() BCНЛABгкЕуMЃЌЙ§ЕуQзїQN
BCНЛABгкЕуMЃЌЙ§ЕуQзїQN![]() BCЃЌДЙзуЮЊЕуNЃЌСЌНгMQЃЌШєЩшдЫЖЏЪБМфЮЊt(s)(0<t<3)ЃЌНтД№ЯТСаЮЪЬтЃК
BCЃЌДЙзуЮЊЕуNЃЌСЌНгMQЃЌШєЩшдЫЖЏЪБМфЮЊt(s)(0<t<3)ЃЌНтД№ЯТСаЮЪЬтЃК
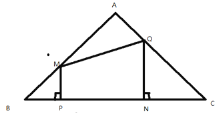
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЕуMЪЧБпABжаЕу?
ЃЈ2ЃЉЩшЫФБпаЮPNQMЕФУцЛ§ЮЊy(cm2)ЃЌЧѓГіyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙSЫФБпаЮPNQM:SЁїABC=4:9?ШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮPNQMЮЊе§ЗНаЮ?ШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉЕБtЮЊ![]() sЪБЃЌЕуMЪЧABжаЕуЃЛ
sЪБЃЌЕуMЪЧABжаЕуЃЛ
ЃЈ2ЃЉyгыtЕФКЏЪ§ЙиЯЕЪНЪЧy![]()
ЃЈ3ЃЉtЕФжЕЮЊ![]() sЃЛ
sЃЛ
ЃЈ4ЃЉВЛДцдкЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіBDЃН3ЃЌИљОн![]() ЃЌМДПЩЧѓГіЪБМфtЃЛ
ЃЌМДПЩЧѓГіЪБМфtЃЛ
ЃЈ2ЃЉЯШХаЖЯГіЁїMBPЁзЁїABDЃЌНјЖјЕУГіMPЃЌЭЌРэБэЪОГіQNКЭCNЃЌШЛКѓРћгУЬнаЮУцЛ§ЙЋЪННјааМЦЫуМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЫљЧѓЃЌНсКЯУцЛ§жЎМфЕФЙиЯЕНЈСЂЗНГЬМДПЩЕУГіНсТлЃЛ
ЃЈ4ЃЉМйЩшДцдкЃЌЯШРћгУPMЃНQNЧѓГіtЃЌНјЖјЧѓГіPMЃЌPNЃЌХаЖЯГіPMЁйPNМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуAзїADЁЭBCгкЕуDЃЌ
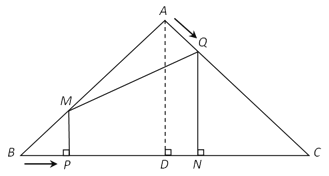
ЁпPMЁЭBCЃЌ
ЁрPMЁЮADЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуMЪЧABжаЕу
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпAB = ACЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBP=tЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
МДЕБtЮЊ![]() sЪБЃЌЕуMЪЧABжаЕуЃЛ
sЪБЃЌЕуMЪЧABжаЕуЃЛ
ЃЈ2ЃЉЙ§ЕуAзїADЁЭBCгкЕуDЃЌ
ЁпPMЁЮADЃЌ
ЁрЁїMBPЁзЁїABDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЭЌРэЃЌЁїQCNЁзЁїACDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрy =SЫФБпаЮPNQM=![]() ЃЌ
ЃЌ
МДyгыtЕФКЏЪ§ЙиЯЕЪНЪЧy![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєSЫФБпаЮPNQM ЃКSЁїABCЃН4ЃК9ЃЌдђy=![]() SЁїABCЃЌ
SЁїABCЃЌ
ЁпSЁїABC=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЁрtЕФжЕЮЊ![]() sЃЛ
sЃЛ
ЃЈ3ЃЉШєЫФБпаЮPNQMЮЊе§ЗНаЮЃЌдђашТњзуPM = QNЃЌPM = PNЃЌ
ЕБPM = QNЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌPM =
ЪБЃЌPM =![]() ЃЌPN=
ЃЌPN=![]() ЃЌ
ЃЌ
ЁрPMЁйPNЃЌ
ЁрВЛДцдкЃЎ


 ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЮЊЁбOЩЯвЛЕуЃЌЁЯABCЕФЦНЗжЯпНЛЁбOгкЕуDЃЌDEЁЭBCгкЕуEЃЎ
ЃЈ1ЃЉЪдХаЖЯDEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDFЁЭABгкЕуFЃЌШєBE=3![]() ЃЌDF=3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌDF=3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
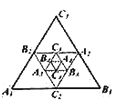
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ5ЃЌ1ЃЉЃЌBЃЈЉ2ЃЌ2ЃЉЃЌCЃЈЉ1ЃЌ4ЃЉЃЌЧыАДЯТСавЊЧѓЛЭМЃК
ЃЈ1ЃЉНЋЁїABCЯШЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЁЂдйЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГігыЁїABCЙигкдЕуOГЩжааФЖдГЦЕФЁїA2B2C2ЃЌВЂжБНгаДГіЕуA2ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁКьзїГіСЫБпГЄЮЊ1ЕФЕк1ИіЕШБп![]() ЃЌЫуГіСЫЕШБп
ЃЌЫуГіСЫЕШБп![]() ЕФУцЛ§ЃЌШЛКѓЗжБ№ШЁ
ЕФУцЛ§ЃЌШЛКѓЗжБ№ШЁ![]() Ш§БпЕФжаЕу
Ш§БпЕФжаЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌзїГіСЫЕк2ИіЕШБп
ЃЌзїГіСЫЕк2ИіЕШБп![]() ЃЌЫуГіСЫЕШБп
ЃЌЫуГіСЫЕШБп![]() ЕФУцЛ§ЃЌгУЭЌбљЕФЗНЗЈЃЌзїГіСЫЕк3ИіЕШБп
ЕФУцЛ§ЃЌгУЭЌбљЕФЗНЗЈЃЌзїГіСЫЕк3ИіЕШБп![]() ЃЌЫуГіСЫЕШБп
ЃЌЫуГіСЫЕШБп![]() ЕФУцЛ§ЁЁЃЌгЩДЫПЩЕУЃЌЕк
ЕФУцЛ§ЁЁЃЌгЩДЫПЩЕУЃЌЕк![]() ИіЕШБп
ИіЕШБп![]() ЕФУцЛ§ЪЧЃЈ ЃЉ
ЕФУцЛ§ЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
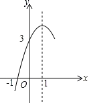
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖдГЦжсЮЊжБЯп
ЕФЖдГЦжсЮЊжБЯп![]() ЃЌгы
ЃЌгы![]() жсвЛИіНЛЕуЕФзјБъЮЊЃЈ-1,0ЃЉЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃК
жсвЛИіНЛЕуЕФзјБъЮЊЃЈ-1,0ЃЉЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃК
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЗНГЬ
ЗНГЬ![]() ЕФСНИіИљЪЧ
ЕФСНИіИљЪЧ![]() ЃЌ
ЃЌ![]() ЃЛЂмЕБ
ЃЛЂмЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() .ЦфжаНсТле§ШЗЕФЪЧ_____________ЃЈЬюаДе§ШЗНсТлЕФБъКХЃЉ
.ЦфжаНсТле§ШЗЕФЪЧ_____________ЃЈЬюаДе§ШЗНсТлЕФБъКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгУЗХДѓОЕПДЁїABCЃЌШєБпBCЕФГЄЖШБфЮЊдРДЕФ2БЖЃЌФЧУДЯТСаЫЕЗЈжаЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉЃЎ
A.БпABЕФГЄЖШвВБфЮЊдРДЕФ2БЖЃЛB.ЁЯBACЕФЖШЪ§вВБфЮЊдРДЕФ2БЖЃЛ
C.ЁїABCЕФжмГЄБфЮЊдРДЕФ2БЖЃЛD.ЁїABCЕФУцЛ§БфЮЊдРДЕФ4БЖЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪщЗЈЪЧЮвЙњЕФЮФЛЏЙхБІЃЌбаЯАЪщЗЈФмХрбјИпбХЕФЦЗИёЃЎФГаЃЮЊМгЧПЪщЗЈНЬбЇЃЌСЫНтбЇЩњЯжгаЕФЪщаДФмСІЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааВтЪдЃЌВтЪдНсЙћЗжЮЊгХауЁЂСМКУЁЂМАИёЁЂВЛМАИёЫФИіЕШМЖЃЌЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЌВЂНЋВтЪдНсЙћЛцжЦГЩШчЭМСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
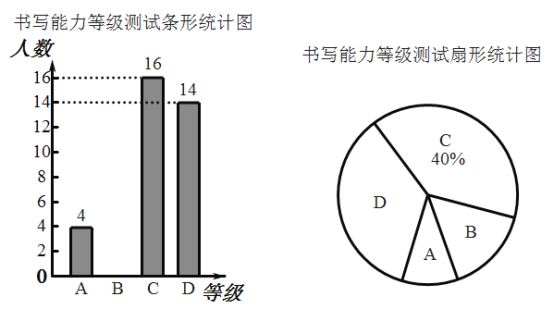
ЧыИљОнЭГМЦЭМжаЕФаХЯЂНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщШЁЕФбЇЩњШЫЪ§ЪЧ ШЫЃЌЩШаЮЭГМЦЭМжаAЫљЖдгІЩШаЮдВаФНЧЕФЖШЪ§ЪЧ ЃЎ
ЃЈ2ЃЉАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉШєИУбЇаЃЙВга2800ШЫЃЌЕШМЖДяЕНгХауЕФШЫЪ§ДѓдМгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛаЃдАЮФЛЏЩњЛюЃЌЬсИпбЇЩњЕФзлКЯЫижЪЃЌДйНјжабЇЩњШЋУцЗЂеЙЃЌбЇаЃПЊеЙСЫЖржжЩчЭХЛюЖЏЃЎаЁУїЯВЛЖЕФЩчЭХгаЃККЯГЊЩчЭХЁЂзуЧђЩчЭХЁЂЪщЗЈЩчЭХЁЂПЦММЩчЭХЃЈЗжБ№гУзжФИAЃЌBЃЌCЃЌDвРДЮБэЪОетЫФИіЩчЭХЃЉЃЌВЂАбетЫФИізжФИЗжБ№аДдкЫФеХЭъШЋЯрЭЌЕФВЛЭИУїЕФПЈЦЌЕФе§УцЩЯЃЌШЛКѓНЋетЫФеХПЈЦЌБГУцГЏЩЯЯДдШКѓЗХдкзРУцЩЯЃЎ
ЃЈ1ЃЉаЁУїДгжаЫцЛњГщШЁвЛеХПЈЦЌЪЧзуЧђЩчЭХBЕФИХТЪЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉаЁУїЯШДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧТМЯТПЈЦЌЩЯЕФзжФИКѓВЛЗХЛиЃЌдйДгЪЃгрЕФПЈЦЌжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧТМЯТПЈЦЌЩЯЕФзжФИЃЎЧыФугУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓГіаЁУїСНДЮГщШЁЕФПЈЦЌжагавЛеХЪЧПЦММЩчЭХDЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯB=60ЃЌЁЯACB=75ЃЌЕуDЪЧBCБпЩЯвЛЖЏЕуЃЌвдADЮЊжБОЖзїЁбOЃЌЗжБ№НЛABЁЂACгкEЁЂFЃЌШєЯвEFЕФзюаЁжЕЮЊ1ЃЌдђABЕФГЄЮЊ
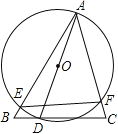
AЃЎ | BЃЎ | CЃЎ1.5 | DЃЎ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com