
 25、如图1,OP是∠MON的平分线,请你在该图形上利用尺规作出一对以OP所在直线为对称轴的全等三角形.
25、如图1,OP是∠MON的平分线,请你在该图形上利用尺规作出一对以OP所在直线为对称轴的全等三角形. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 3)是反比例函数图象上的点:
3)是反比例函数图象上的点:查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 | 5 |

查看答案和解析>>
科目:初中数学 来源:北京同步题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市闸北区中考一模数学试卷(解析版) 题型:解答题
(本题满分14分 第(1)小题4分,第(2)小题4分,第(3)小题6分)
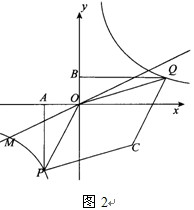
已知:如图,在△ABC中,AB=AC=15, cos∠A= .点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.
.点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.

(1)求底边BC的长;
(2)若点O是BC的中点,联接MP、MO、OP,设四边形AMOP的面积是y,求y关于x的函数关系式,并出写出x的取值范围;
(3)把△MPA沿着直线MP翻折后得到△MPN,是否可能使△MPN的一条边(折痕边PM除外)与AC垂直?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com