
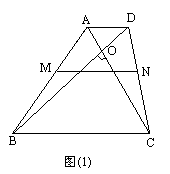
如图(1),在梯形ABCD中,AD∥BC,对角钱AC与BD垂直相交于O,MN是梯形ABCD的中位线,∠DBC=![]() .
.
求证:AC=MN
|
解析:分析1:将AC平移至DE的位置,将梯形中的问题转化为△BDE中的问题 证法1:如图(2),过D点作DE∥AC交BC的延长线于E.∴AC⊥BD于O,∴∠BDE=∠BOC=
∴CE=AD,DE=AC ① 在Rt△BDE中,∵∠DBE= ∴DE= = ∵MN是梯形ABCD的中位线, ∴MN= 由①、②得:MN=AC 分析2:欲证AC= 证法2:∵AC与BD垂直相交于O, ∴△BOC与△AOD都是直角三角形 在Rt△BOC中,∵∠OBC= ∴OC= ∴∠ADO=∠OBC= 故同理有AO= ∴AC=AO+OC= ∵MN是梯形ABCD的中位线, ∴MN= |


科目:初中数学 来源: 题型:
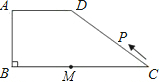 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有查看答案和解析>>
科目:初中数学 来源: 题型:
 知AB=8,边BC比AD大6.
知AB=8,边BC比AD大6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com