
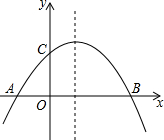
 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.分析 (1)把C坐标代入抛物线解析式求出m的值即可;
(2)①对于抛物线解析式,令y=0求出x的值,确定出A与B坐标;令x=0,求出y的值,确定出C坐标,求出三角形ABC面积即可;
②如图1,连接BC交对称轴于点H,由对称轴的性质和两点之间线段最短的性质可得:此时AH+CH=BH+CH=BC最小,利用待定系数法求出直线BC解析式,与抛物线对称轴联立求出H坐标即可;
(3)在第四象限内,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似,分两种情况考虑:(i)当△ACB∽△ABM时;(ii)当△ACB∽△MBA时,利用相似三角形的判定与性质,确定出m的值即可.
解答 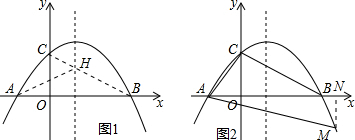 解:(1)∵抛物线过G(2,2),
解:(1)∵抛物线过G(2,2),
∴把G坐标代入抛物线解析式得:2=-$\frac{1}{m}$(2+2)(2-m),
解得:m=4;
(2)①令y=0,得到-$\frac{1}{m}$(x+2)(x-m)=0,
解得:x1=-2,x2=m,
∵m>0,
∴A(-2,0),B(m,0),
把m=4代入得:B(4,0),
∴AB=6,
令x=0,得到y=2,即C(0,2),
∴OC=2,
则S△ABC=$\frac{1}{2}$×6×2=6;
②∵A(-2,0),B(4,0),
∴抛物线解析式为y=-$\frac{1}{4}$(x+2)(x-4)的对称轴为x=1,
如图1,连接BC交对称轴于点H,由对称轴的性质和两点之间线段最短的性质可得:此时AH+CH=BH+CH=BC最小,
设直线BC的解析式为y=kx+b,
把B与C坐标代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线BC解析式为y=-$\frac{1}{2}$x+2,
令x=1,得到y=$\frac{3}{2}$,即H(1,$\frac{3}{2}$);
(3)在第四象限内,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似,
分两种情况考虑:
(i)当△ACB∽△ABM时,则有$\frac{AC}{AB}$=$\frac{AB}{AM}$,即AB2=AC•AM,
∵A(-2,0),C(0,2),即OA=OC=2,
∴∠CAB=45°,∠BAM=45°,
如图2,过M作MN⊥x轴,交x轴于点N,则AN=MN,
∴OA+ON=2+ON=MN,
设M(x,-x-2)(x>0),
把M坐标代入抛物线解析式得:-x-2=-$\frac{1}{m}$(x+2)(x-m),
∵x>0,∴x+2>0,
∵m>0,∴x=2m,即M(2m,-2m-2),
∴AM=$\sqrt{(2m+2)^{2}+(-2m-2)^{2}}$=2$\sqrt{2}$(m+1),
∵AB2=AC•AM,AC=2$\sqrt{2}$,AB=m+2,
∴(m+2)2=2$\sqrt{2}$•2$\sqrt{2}$(m+1),
解得:m=2±2$\sqrt{2}$,
∵m>0,
∴m=2+2$\sqrt{2}$;
(ii)当△ACB∽△MBA时,则$\frac{AB}{MA}$=$\frac{CB}{BA}$,即AB2=CB•MA,
∵∠CBA=∠BAM,∠ANM=∠BOC=90°,
∴△ANM∽△BOC,
∴$\frac{NM}{AN}$=$\frac{OC}{BO}$,
∵OB=m,设ON=x,
∴$\frac{NM}{2+x}$=$\frac{2}{m}$,即MN=$\frac{2}{m}$(x+2),
令M(x,-$\frac{2}{m}$(x+2))(x>0),
把M坐标代入抛物线解析式得:-$\frac{2}{m}$(x+2)=-$\frac{1}{m}$(x+2)(x-m),
∵x>0,∴x+2>0,
∵m>0,∴x=m+2,即M(m+2,-$\frac{2}{m}$(m+4)),
∵AB2=CB•MA,CB=$\sqrt{{m}^{2}+4}$,AN=m+4,MN=$\frac{2}{m}$(m+4),
∴(m+2)2=$\sqrt{{m}^{2}+4}$•$\sqrt{(m+4)^{2}+\frac{4(m+4)^{2}}{{m}^{2}}}$,
整理得:$\frac{16}{m}$=0,显然不成立,
综上,在第四象限内,当m=2$\sqrt{2}$+2时,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似.
点评 此题属于二次函数综合题,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,相似三角形的判定与性质,勾股定理,以及两点之间线段最短,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
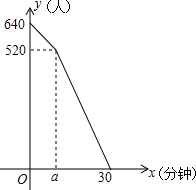 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
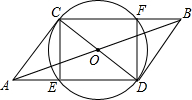 如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解我国中学生的体能情况,应采用普查的方式 | |
| B. | 若甲队成绩的方差是2,乙队成绩的方差是3,说明甲队成绩比乙队成绩稳定 | |
| C. | 明天下雨的概率是99%,说明明天一定会下雨 | |
| D. | 一组数据4,6,7,6,7,8,9的中位数和众数都是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
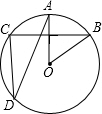 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
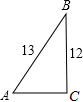 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )| A. | sinA=$\frac{12}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{5}{12}$ | D. | tanB=$\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com