
如图,在梯形纸片ABCD中,BC∥AD,∠A+∠D=90°,tanA=2,过点B作BH⊥AD与H,BC=BH=2.动点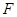 从点
从点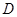 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿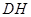 运动到点
运动到点 停止,在运动过程中,过点
停止,在运动过程中,过点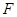 作
作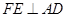 交折线
交折线 于点
于点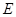 ,将纸片沿直线
,将纸片沿直线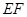 折叠,点
折叠,点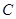 、
、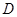 的对应点分别是点
的对应点分别是点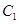 、
、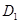 。设
。设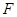 点运动的时间是
点运动的时间是 秒(
秒(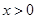 )。
)。
(1)当点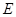 和点
和点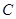 重合时,求运动时间
重合时,求运动时间 的值;
的值;
(2)在整个运动过程中,设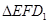 或四边形
或四边形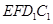 与梯形
与梯形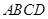 重叠部分面积为
重叠部分面积为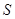 ,请直接写出
,请直接写出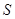 与
与 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量 的取值范围;
的取值范围;
(3)平移线段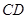 ,交线段
,交线段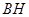 于点
于点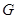 ,交线段
,交线段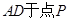 。在直线
。在直线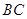 上存在点
上存在点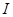 ,使
,使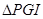 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段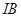 的所有可能的长度。
的所有可能的长度。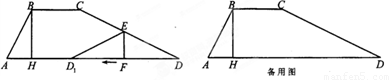
(1)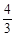 (2)0(3)
(2)0(3)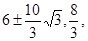
【解析】
试题分析:(1)t+1,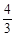
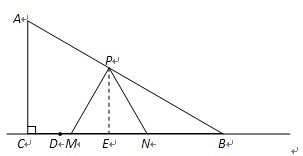
△PMN的边长MN=CN-CM=CD+DN-CM=1+2t-t=t+1.
当点P落在AB上时,过P作PE⊥MN于E.则CE=CM+ME=t+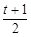 =
=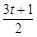
∴BE=6-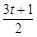 =
=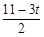 .∵等边△PMN,MN=t+1,
.∵等边△PMN,MN=t+1,
∴PE=PN·sin60°=MN·sin60°= (t+1).
(t+1).
在△ABC中,∠ACB=90°,∠ABC=30°,BC=6.∴AC=BC·tan30°=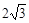 .
.
∵∠PEB=∠ACB=90°,∠PBE=∠ABC.∴△PBE∽△ABC,∴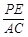 =
=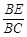 .
.
即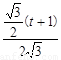 =
=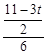 ,解得t=
,解得t=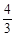
(2)当0<t≤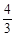 时,△PMN在△ABC内部.
时,△PMN在△ABC内部.
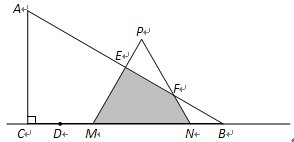
∴S=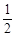 ×(t+1)×
×(t+1)× (t+1)=
(t+1)=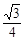 (t+1)2
(t+1)2
点N从点D运动到与点B重合所需时间为: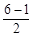 =
=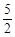 (秒)
(秒)
当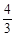 <t<
<t<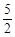 时,△PMN与△ABC重叠部分为四边形EFNM.
时,△PMN与△ABC重叠部分为四边形EFNM.
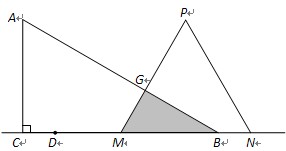
∵∠PNM=60°,∠ABC=30°,∴∠NFB=∠ABC=30°.∴NF=NB=6-(2t+1)=5-2t
∴PF=(t+1)-(5-2t)=3t-4,∵∠NFB=30°,∴∠PFE=30°.
∵∠P=60°,∴∠PEF=90°,∴PE=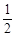 PF=
PF=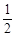 (3t-4),EF=
(3t-4),EF= PF=
PF= (3t-4).
(3t-4).
∴S△PEF =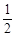 EF·PE=
EF·PE=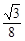 (3t-4)2
(3t-4)2
∴S=S△PMN -S△PEF =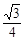 (t+1)2-
(t+1)2-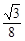 (3t-4)2
(3t-4)2
=-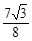 t2+
t2+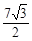 t-
t-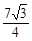 .
.
当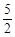 ≤t<6时,△PMN与△ABC重叠部分为△GMB.在Rt△GMB中,∠GBM=30°,MB=6-t.
≤t<6时,△PMN与△ABC重叠部分为△GMB.在Rt△GMB中,∠GBM=30°,MB=6-t.
∴GM=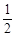 MB=
MB=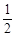 (6-t),GB=
(6-t),GB= MB=
MB= (6-t)
(6-t)
∴S=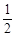 GM·GB=
GM·GB=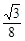 (6-t)2当t≥6时,S=0.
(6-t)2当t≥6时,S=0.
(3)设BC1=X,BL=y,G在BH上,则有
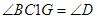
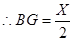
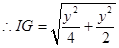
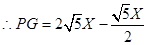
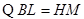
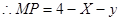
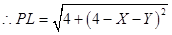
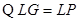
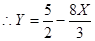
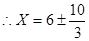
当LG=GP时
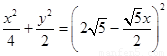
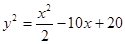
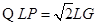
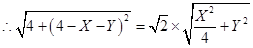
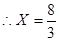
考点:二次函数的综合题
点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 17、如图,在梯形纸片ABCD中,AB∥CD,AD=BC,AB=6,CD=3.将该梯形纸片沿对角线AC折叠,点D恰与AB边上的点E重合,则∠BCE=
17、如图,在梯形纸片ABCD中,AB∥CD,AD=BC,AB=6,CD=3.将该梯形纸片沿对角线AC折叠,点D恰与AB边上的点E重合,则∠BCE=查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2010-2011学年七年级下学期期末考试数学试题 题型:022
如图,在梯形纸片ABCD中,AB∥CD,AD=BC,AB=6,CD=3.将该梯形纸片沿对角线AC折叠,点D恰与AB边上的点E重合,则∠BCE=_________度.

查看答案和解析>>
科目:初中数学 来源:2012年广东省深圳市外国语学校中考数学模拟试卷(3月份)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:江苏省期末题 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在梯形纸片ABCD中,AB∥CD,AD=BC,AB=6,CD=3.将该梯形纸片沿对角线AC折叠,点D恰与AB边上的点E重合,则∠BCE= 度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com