
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
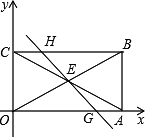
(1)①直接写出点E的坐标:________;②求证:AG=CH.
(2)如下图,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
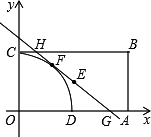
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
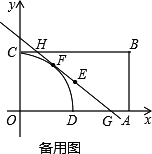
|
分析:(1)①根据矩形的性质和边长即可求出E的坐标;②推出CE=AE,BC∥OA,推出∠HCE=∠EAG,证出△CHE≌△AGE即可; (2)连接DE并延长DE交CB于M,求出DD=OC= (3)连接BG,证△OCH≌△BAG,求出∠CHO=∠AGB,证△HOE≌△GBE,求出∠OHE=∠BGE,得出BG平分∠FGA,推出圆心P必在BG上,过P做PN⊥GA,垂足为N,根据△GPN∽△GBA,得出 解答:(1)①解:E的坐标是:(1, 故答案为:(1, ②证明:∵矩形OABC, ∴CE=AE,BC∥OA, ∴∠HCE=∠EAG, ∵在△CHE和△AGE中 ∴△CHE≌△AGE, ∴AG=CH. (2)解:连接DE并延长DE交CB于M, ∵DD=OC=1= ∴D是OA的中点, ∵在△CME和△ADE中 ∴△CME≌△ADE, ∴CM=AD=2-1=1, ∵BC∥OA,∠COD=90°, ∴四边形CMDO是矩形, ∴MD⊥OD,MD⊥CB, ∴MD切⊙O于D, ∵得HG切⊙O于F,E(1, ∴可设CH=HF=x,FE=ED= 在Rt△MHE中,有MH2+ME2=HE2 即(1-x)2+( 解得x= ∴H( 又∵G( 设直线GH的解析式是:y=kx+b, 把G、H的坐标代入得:0=b,且1= 解得:k=- ∴直线GH的函数关系式为y=- (3)答:⊙P的半径是 解:连接BG, ∵在△OCH和△BAG中 ∴△OCH≌△BAG, ∴∠CHO=∠AGB, ∵∠HCO=90°, ∴HC切⊙O于C,HG切⊙O于F, ∴OH平分∠CHF, ∴∠CHO=∠FHO=∠BGA, ∵△CHE≌△AGE, ∴HE=GE, 在△HOE和△GBE中 ∴△HOE≌△GBE, ∴∠OHE=∠BGE, ∵∠CHO=∠FHO=∠BGA, ∴∠BGA=∠BGE, 即BG平分∠FGA, ∵⊙P与HG、GA、AB都相切, ∴圆心P必在BG上, 过P做PN⊥GA,垂足为N, ∴△GPN∽△GBA, ∴ 设半径为r, 解得:r=
点评:本题综合考查了矩形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,切线的性质和判定,一次函数和勾股定理等知识点,本题综合性比较强,难度偏大,但是也是一道比较好的题目. |
|
切线的判定与性质;一次函数综合题;全等三角形的判定与性质;勾股定理;矩形的性质;相似三角形的判定与性质. |


科目:初中数学 来源: 题型:
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com