
ЁОЬтФПЁПШчЭМЃЌЕШБпЁїAOBжаЕуOЪЧдЕуЃЌЕуAдкyжсЩЯЃЌЕуBЕФзјБъЪЧЃЈ2 ![]() ЃЌ2ЃЉЃЌаЁУїзівЛИіЪ§бЇЪЕбщЃЌдкxжсЩЯШЁвЛЖЏЕуCЃЌвдACЮЊвЛБпЛГіЕШБпЁїACPЃЌвЦЖЏЕуCЪБЃЌЬНОПЕуPЕФЮЛжУБфЛЏЧщПіЃЎ
ЃЌ2ЃЉЃЌаЁУїзівЛИіЪ§бЇЪЕбщЃЌдкxжсЩЯШЁвЛЖЏЕуCЃЌвдACЮЊвЛБпЛГіЕШБпЁїACPЃЌвЦЖЏЕуCЪБЃЌЬНОПЕуPЕФЮЛжУБфЛЏЧщПіЃЎ
ЃЈ1ЃЉШчЭМЃЌаЁУїНЋЕуCвЦжСxжсИКАыжсЃЌдкACЕФгвВрЛГіЕШБпЁїACPЃЌВЂЪЙЕУЖЅЕуPдкЕкШ§ЯѓЯоЪБЃЌСЌНгBPЃЌЧѓжЄЃКЁїAOCЁеЁїABPЃЛ
ЃЈ2ЃЉаЁУїдкxжсЩЯвЦЖЏЕуCЃЌВЂдкACЕФгвВрЛГіЕШБпЁїACPЪБЃЌЗЂЯжЕуPдкФГКЏЪ§ЭМЯѓЩЯЃЌЧыЧѓГіЕуPЫљдкКЏЪ§ЭМЯѓЕФНтЮіЪНЃЎ
ЃЈ3ЃЉаЁУїдкxжсЩЯвЦЖЏЕуCЕуЪБЃЌШєдкACЕФзѓВрЛГіЕШБпЁїACPЃЌЕуPЛсВЛЛсдкФГКЏЪ§ЭМЯѓЩЯЃПШєЛсдкФГКЏЪ§ЭМЯѓЩЯЃЌЧыжБНгаДГіИУКЏЪ§ЭМЯѓЕФНтЮіЪНЃЌШєВЛдкФГКЏЪ§ЭМЯѓЩЯЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
жЄУїЃКШчЭМЃЌ
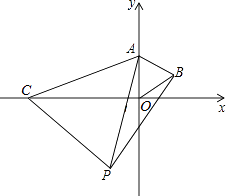
ЁпЁїAOBгыЁїACPЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрOA=ABЃЌA=APЃЌCAP=ЁЯOAB=60ЁуЃЎ
ЁрЁЯCAP+ЁЯPAO=ЁЯOAB+ЁЯPAOЃЎ
ЁрЁЯCAO=ЁЯPABЃЎ
дкЁїAOCгыЁїPABжаЃЌ
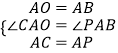 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїABP
ЃЈ2ЃЉ
НтЃКгЩЃЈ1ЃЉПЩжЊЃЌЁїAOCЁеЁїABPЃЌ
ЁрЁЯCOA=ЁЯPBA=90ЁуЃЌ
ЁрЕуPдкЙ§ЕуAЧвгыABДЙжБЕФжБЯпЩЯЃЌ
дкЕШБпЁїAOBжаЃЌBЃЈ2 ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
ЁрAB=4ЃЌ
ЕБЕуCвЦЖЏЃЌЪЙЕУPдкyжсЩЯЪБЃЌ
ЁпЁїPABЪЧжБНЧШ§НЧаЮЃЌЁЯPAB=60ЁуЃЌ
ЁрPA= ![]() =8ЃЌ
=8ЃЌ
ЁрPЃЈ0ЃЌЉ4ЃЉЃЌ
ЩшжБЯпPBЕФНтЮіЪНЮЊy=kxЉ4ЃЌАбBЃЈ2 ![]() ЃЌ2ЃЉДњШыЕУЕНk=
ЃЌ2ЃЉДњШыЕУЕНk= ![]() ЃЌ
ЃЌ
ЁрЕуPЫљдкКЏЪ§ЭМЯѓЕФНтЮіЪНЮЊy= ![]() xЉ4
xЉ4
ЃЈ3ЃЉ
ЛсдкКЏЪ§ЕФЭМЯѓЩЯЃЌШчЭМзїBЕФЖдГЦЕуBЁфЃЌСЌНгABЁфЃЌOBЁфЃЎ
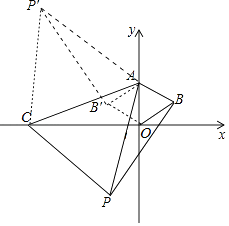
гЩЃЈ2ЃЉПЩжЊЃЌPЁфBЁфЁЭABЁфЃЌЭЌЗЈПЩЕУжБЯпPЁфBЁфЕФНтЮіЪНЮЊt=Љ ![]() xЉ4ЃЎ
xЉ4ЃЎ
ЁрИУКЏЪ§ЭМЯѓЕФНтЮіЪНЮЊy=Љ ![]() xЉ4
xЉ4
ЁОНтЮіЁПЃЈ1ЃЉРћгУЕШБпШ§НЧаЮЕФаджЪЃЌИљОнSASИљОнНтОіЮЪЬтЃЎЃЈ2ЃЉЪзЯШжЄУїЕуPдкЙ§ЕуAЧвгыABДЙжБЕФжБЯпЩЯЃЌЧѓГіЬиЪтЕуЃЈPдкyжсЩЯЕФЕуЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЎЃЈ3ЃЉШчЭМзїBЕФЖдГЦЕуBЁфЃЌСЌНгABЁфЃЌOBЁфЃЎгЩЃЈ2ЃЉПЩжЊЃЌPЁфBЁфЁЭABЁфЃЌЭЌЗЈПЩЕУжБЯпPЁфBЁфЕФНтЮіЪНЮЊt=Љ ![]() xЉ4ЃЎ
xЉ4ЃЎ
ЁОПМЕуОЋЮіЁПЭЈЙ§СщЛюдЫгУЕШБпШ§НЧаЮЕФаджЪЃЌеЦЮеЕШБпШ§НЧаЮЕФШ§ИіНЧЖМЯрЕШВЂЧвУПИіНЧЖМЪЧ60ЁуМДПЩвдНтД№ДЫЬтЃЎ


 дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ
дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ
ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() ШчЭМ
ШчЭМ![]() ЫљЪОЃЌдк
ЫљЪОЃЌдк![]() жаЃЌ
жаЃЌ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЕФжмГЄ
ЕФжмГЄ![]() ЃЛ21.
ЃЛ21.
![]() ШчЭМ
ШчЭМ![]() ЫљЪОЃЌдк
ЫљЪОЃЌдк![]() жаЃЌШє
жаЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
![]() ШчЭМ
ШчЭМ![]() ЫљЪОЃЌдк
ЫљЪОЃЌдк![]() жаЃЌШє
жаЃЌШє![]() ЃЌ
ЃЌ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈЉ2ЃЌ0ЃЉЃЌCЃЈ2ЃЌ2ЃЉЃЌЙ§CзїCBЁЭxжсгкBЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЁїABCЕФУцЛ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкyжсЩЯеввЛЕуPЃЌЪЙЕУЁїABPЕФУцЛ§гыЁїABCЕФУцЛ§ЯрЕШЃЌЧыжБНгаДГіPЕузјБъЃКЁЁ ЁЁЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЙ§BзїBDЁЮACНЛyжсгкDЃЌдђЁЯBAC+ЁЯODBЕФЖШЪ§ЮЊЁЁ ЁЁЖШЃЛ
ЃЈ4ЃЉШчЭМ3ЃЌBDЁЮACЃЌШєAEЁЂDEЗжБ№ЦНЗжЁЯCABЃЌЁЯODBЃЌЧѓЁЯAEDЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌaЪЧ
ЃЌaЪЧ![]() ЕФСЂЗНИљЃЌЗНГЬ
ЕФСЂЗНИљЃЌЗНГЬ![]() ЪЧЙигкxЃЌyЕФЖўдЊвЛДЮЗНГЬЃЌdЮЊВЛЕШЪНзщ
ЪЧЙигкxЃЌyЕФЖўдЊвЛДЮЗНГЬЃЌdЮЊВЛЕШЪНзщ![]() ЕФзюДѓећЪ§НтЃЎ
ЕФзюДѓећЪ§НтЃЎ
![]() ЧѓЕуAЁЂBЁЂCЕФзјБъЃЛ
ЧѓЕуAЁЂBЁЂCЕФзјБъЃЛ
![]() ШчЭМ1ЃЌШєDЮЊyжсИКАыжсЩЯЕФвЛИіЖЏЕуЃЌЕБ
ШчЭМ1ЃЌШєDЮЊyжсИКАыжсЩЯЕФвЛИіЖЏЕуЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ЕФЦНЗжЯпНЛгкMЕуЃЌЧѓ
ЕФЦНЗжЯпНЛгкMЕуЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
![]() ШчЭМ2ЃЌШєDЮЊyжсИКАыжсЩЯЕФвЛИіЖЏЕуЃЌСЌBDНЛxжсгкЕуEЃЌЮЪЪЧЗёДцдкЕуDЃЌЪЙ
ШчЭМ2ЃЌШєDЮЊyжсИКАыжсЩЯЕФвЛИіЖЏЕуЃЌСЌBDНЛxжсгкЕуEЃЌЮЪЪЧЗёДцдкЕуDЃЌЪЙ![]() ЃПШєДцдкЃЌЧыЧѓГіDЕФзнзјБъ
ЃПШєДцдкЃЌЧыЧѓГіDЕФзнзјБъ![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDНјааелжНЃЌвбжЊИУжНЦЌПэABЮЊ8cmЃЌГЄBCЮЊ10cmЃЌЕБбиAEелЕўЪБЃЌЖЅЕуDТфдкBCБпЩЯЕФЕуFДІЃЌЪдЧѓCEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЙцЖЈАбвЛИіЕуЯШШЦдЕуФцЪБеыа§зЊ45ЁуЃЌдйзїГіЫќЙигкдЕуЕФЖдГЦЕуГЦЮЊвЛДЮБфЛЛЃЌвбжЊЕуAЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌАбЕуAОЙ§СЌај2014ДЮетбљЕФБфЛЛЕУЕНЕФЕуA2014ЕФзјБъЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйa+b+cЃМ0ЃЛЂкaЉb+cЃМ0ЃЛЂлb+2aЃМ0ЃЛЂмabcЃО0ЃЌЦфжае§ШЗЕФЪЧЃЈЬюБрКХЃЉ 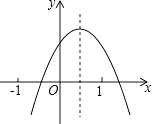
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїACBКЭЁїECDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯECD=90ЁуDЮЊABБпЩЯвЛЕу.
ЧѓжЄЃКЃЈ1ЃЉЁїACE![]() ЁїBCDЃЛ
ЁїBCDЃЛ
ЃЈ2ЃЉ![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЭјИёжаУПвЛИіаЁе§ЗНаЮЕФБпГЄЮЊ1ИіЕЅЮЛГЄЖШЃЛвбжЊЁїABCЃЎ 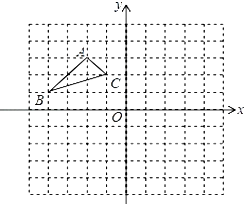
ЃЈ1ЃЉзїГіЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1 ЃЌ ЃЈжЛЛГіЭМаЮЃЉЃЎ
ЃЈ2ЃЉзїГіЁїABCЙигкдЕуOГЩжааФЖдГЦЕФЁїA2B2C2 ЃЌ ЃЈжЛЛГіЭМаЮЃЉЃЌаДГіB2КЭC2ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com