练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    证明：（x+y+z）3xyz-（yz+zx+xy）3=xyz（x3+y3+z3）-（y3z3+z3x3+x3y3）．
    分析：本题需先根据三数完全平方公式进行展开各式，然后消去同类项，再进行移项，最后证出等于零即可求出结果
    解答：证明：∵（x+y+z）3xyz-（yz+zx+xy）3=xyz（x3+y3+z3）-（y3z3+z3x3+x3y3）
    ∴xyz[（x+y+z）3-（x3+y3+z3）]=（yz+zx+xy）3）-（y3z3+z3x3+x3y3）
    ∴xyz[（x3+y3+z3+3x2y+3xy2+3xz2
    +3y2z
    +3yz2+6xyz）-（x3+y3+z3）]，
    =（y3z3+z3x3+x3y3+3y2z3x+3z3x2y+3y2zx2+3z2x3y+3zx3y2+6y2z2x2）-（y3z3+z3x3+x3y3），
    ∴xyz（3x2y+3xy2+3xz2
    +3y2z
    +3yz2+6xyz）=3y2z3x+3z3x2y+3y2zx2+3z2x3y+3zx3y2+6y2z2x2
    ∴（3x3y2z+3x2y3z+3x2z3y+3y3z2x+3y2z3x+6x2y2z2=3y2z3x+3z3x2y+3y2zx2+3z2x3y+3zx3y2+6y2z2x2
    ∴（3x3y2z+3x2y3z+3x2z3y+3y3z2x+3y2z3x+6x2y2z2-3y2z3x-3z3x2y-3y2zx2-3z2x3y--6y2z2x2=0
    ∴（x+y+z）3xyz-（yz+zx+xy）3=xyz（x3+y3+z3）-（y3z3+z3x3+x3y3）．
    点评：本题主要考查了整式的等式证明，在解题时要注意三数完全立方公式的应用，这是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    22、如图，已知：点B，F，C，D在同一直线上，且FB=CD，AB∥ED，AC∥FE，请你根据上述条件，判断∠A与∠E的大小关系，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

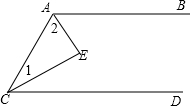    精英家教网如图，AB∥CD，AE平分∠BAC，CE平分∠ACD，求∠E为多少？
    下面是小明同学的解法，请帮助他完成证明．
    证明：因为∠1=∠ECD=
    1
    2
    ∠ACD （原因：
     
    ）
    又因为∠2=（∠BAE　　）=
    1
    2
    ∠CAB（原因：
     
    ）
    又因为AB∥CD，
    所以∠CAB+∠ACD=180°（原因：
     
    ）
    所以∠1+∠2=
    1
    2
    （∠CAB+∠ACD）=90°（等量代换）
    又因为∠1+∠2+∠E=180°（原因：
     
    ）
    所以∠E=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    对于正数x，规定f（x）=
    x2
    1+x2
    ，
    （1）计算f（2）=
     
    ；f（
    1
    2
    ）=
     
    ；f（2）+f（
    1
    2
    ）=
     
    ；f（3）+f（
    1
    3
    ）=
     
    ；…
    （2）猜想f（x）+f(
    1
    x
    )    =
     
    ，请予以证明．
    （3）现在你会计算f(
    1
    2010
    )    +f（
    1
    2009
    ）+f（
    1
    2008
    ）+f（
    1
    2007
    ）+f（
    1
    2006
    ）+…f（
    1
    3
    ）+f（
    1
    2
    ）+f（1）+f（2）+f（3）+…+f（2006）+f（2007）+f（2008）+f（2009）+f（2010）的值了吗，写出你的计算过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知在Rt△ABC中，∠B=90°，AC=13，AB=5，O是AB上的点，以O为圆心，OB精英家教网为半径作⊙O．
    （1）当OB=2.5时，⊙O交AC于点D，求CD的长；
    （2）当OB=2.4时，AC与⊙O的位置关系如何？试证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    20、如图，AE∥BC，AE平分∠CAD，试说明∠B=∠C
    证明：∵AE∥BC
    已知

    ∴∠1=
    ∠B（两直线平行，同位角相等）

    ∠2=
    ∠C（两直线平行，内错角相等）

    又∵AE平分∠CAD
    ∴∠1=∠2
    角平分线的定义

    ∴∠
    B
    =∠
    C
    ．

    查看答案和解析>>

    同步练习册答案