
【题目】在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() .
.
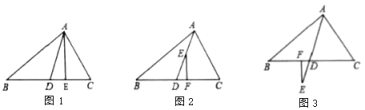
(1)如图1,![]() 是高,
是高,![]() ,
,![]() ,则
,则![]()
![]() (直接写出结论,不需写解题过程);
(直接写出结论,不需写解题过程);
(2)如图2,点![]() 在
在![]() 上,
上,![]() 于
于![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间的数量关系,写出你的探究结论并证明;
之间的数量关系,写出你的探究结论并证明;
(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于
于![]() ,则
,则![]() 与
与![]() 、
、![]() 之间的数量关系是 (直接写出结论,不需证明).
之间的数量关系是 (直接写出结论,不需证明).
【答案】(1) 11;(2) ∠DEF=![]() (∠C-∠B),证明见解析;(3) ∠DEF=
(∠C-∠B),证明见解析;(3) ∠DEF=![]() (∠C-∠B) ,证明见解析
(∠C-∠B) ,证明见解析
【解析】
(1)依据角平分线的定义以及垂线的定义,即可得到∠CAD=![]() ∠BAC,∠CAE=90°-∠C,进而得出∠DAE=
∠BAC,∠CAE=90°-∠C,进而得出∠DAE=![]() (∠C-∠B),由此即可解决问题.
(∠C-∠B),由此即可解决问题.
(2)过A作AG⊥BC于G,依据平行线的性质可得∠DAG=∠DEF,依据(1)中结论即可得到∠DEF=![]() (∠C-∠B).
(∠C-∠B).
(3)过A作AG⊥BC于G,依据平行线的性质可得∠DAG=∠DEF,依据(1)中结论即可得到∠DEF=![]() (∠C-∠B)不变.
(∠C-∠B)不变.
(1)∵AD平分∠BAC,
∴∠CAD=![]() ∠BAC,
∠BAC,
∵AE⊥BC,
∴∠CAE=90°-∠C,
∴∠DAE=∠CAD-∠CAE
=![]() ∠BAC-(90°-∠C)
∠BAC-(90°-∠C)
=![]() (180°-∠B-∠C)-(90°-∠C)
(180°-∠B-∠C)-(90°-∠C)
=![]() ∠C-
∠C-![]() ∠B
∠B
=![]() (∠C-∠B),
(∠C-∠B),
∵∠B=52°,∠C=74°,
∴∠DAE=![]() (74°-52°)=11°;
(74°-52°)=11°;
(2)结论:∠DEF=![]() (∠C-∠B).
(∠C-∠B).
理由:如图2,过A作AG⊥BC于G,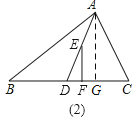
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=![]() (∠C-∠B),
(∠C-∠B),
∴∠DEF=![]() (∠C-∠B);
(∠C-∠B);
(3)仍成立.
如图3,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=![]() (∠C-∠B),
(∠C-∠B),
∴∠DEF=![]() (∠C-∠B),
(∠C-∠B),
故答案为∠DEF=![]() (∠C-∠B).
(∠C-∠B).


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
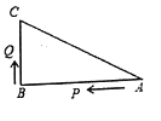
【题目】如图所示,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 的边上的两个动点,其中点
的边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为![]() .
.
(1)则![]() ____________
____________![]() ;
;
(2)当![]() 为何值时,点
为何值时,点![]() 在边
在边![]() 的垂直平分线上?此时
的垂直平分线上?此时![]() _________?
_________?
(3)当点![]() 在边
在边![]() 上运动时,直接写出使
上运动时,直接写出使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
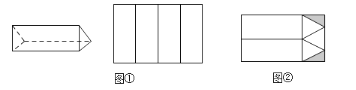
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.
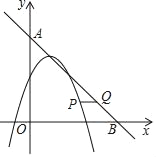
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第一次操作,把抛物线
称为第一次操作,把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第二次操作,…,以此类推,则抛物线
称为第二次操作,…,以此类推,则抛物线![]() 经过第
经过第![]() 此操作后得到的抛物线
此操作后得到的抛物线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()

![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今通过微信朋友圈发布自己每天行走的步数已成为一种时尚.“健身达人”小张为了了解他的微信朋友圈里大家的运动情况,随机抽取了部分好友进行调查,把他们1月29日那天每人行走的步数情况分为五个类别:A(0~4000步)(说明:0~4000表示大于或等于0,小于或等于4000,下同)、B(4001~8000步)、C(8001~12000步)、D(12001~16000步)、E(16000步以上),并将统计结果绘制了如图1和2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)小张随机抽取了 名微信朋友圈好友;
(2)将图1的条形统计图补充完整;
(3)已知小张的微信朋友圈里共300人,请根据本次抽查的结果,估计在它的微信朋友圈里1月29日那天行走不超过8000步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com