
 (1)观察思考
(1)观察思考分析 (1)从左向右依次固定一个端点A,C,D找出线段,最后求和即可;
(2)根据数线段的特点列出式子化简即可;
(3)将实际问题转化成(2)的模型,借助(2)的结论即可得出结论.
解答 解:(1)∵以点A为左端点向右的线段有:线段AB、AC、AD,
以点C为左端点向右的线段有线段CD、CB,
以点D为左端点的线段有线段DB,
∴共有3+2+1=6条线段;
(2)$\frac{m(m-1)}{2}$,
理由:设线段上有m个点,该线段上共有线段x条,
则x=(m-1)+(m-2)+(m-3)+…+3+2+1,
∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1),
∴2x=$\underset{\underbrace{m+m+…+m}}{(m-1)个m}$=m(m-1),
∴x=$\frac{m(m-1)}{2}$;
(3)把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,
直线上8个点所构成的线段条数就等于比赛的场数,
因此一共要进行$\frac{8×(8-1)}{2}$=28场比赛.
点评 此题是线段的计数问题,主要考查了数线段的方法和技巧,解本题的关键是找出规律,此类题目容易数重或遗漏,要特别注意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.
如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A为函数y=$\frac{9}{x}$(x>0)的图象上一点,连接OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积是( )
如图,点A为函数y=$\frac{9}{x}$(x>0)的图象上一点,连接OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积是( )| A. | $\frac{9}{2}$ | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
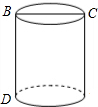 如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程大约为( )
如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程大约为( )| A. | 13cm | B. | 12cm | C. | 6cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
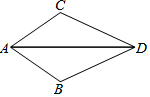 如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )| A. | AB=AC | B. | BD=CD | C. | ∠B=∠C | D. | ∠BAD=∠CAD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com