
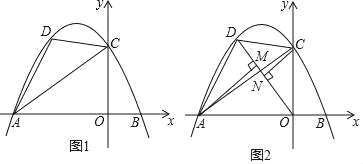
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)点P的坐标为(﹣
x+3;(2)点P的坐标为(﹣![]() ,1);(3)当AM+CN的值最大时,点D的坐标为(
,1);(3)当AM+CN的值最大时,点D的坐标为(![]() ,
,![]() ).
).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,由点B所在的位置结合点B的横坐标可得出点B的坐标,根据点A、B、C的坐标,利用待定系数法即可求出抛物线的函数关系式;
(2)过点P作PE⊥x轴,垂足为点E,则△APE∽△ACO,由△PCD、△PAD有相同的高且S△PCD=2S△PAD,可得出CP=2AP,利用相似三角形的性质即可求出AE、PE的长度,进而可得出点P的坐标;
(3)连接AC交OD于点F,由点到直线垂线段最短可找出当AC⊥OD时AM+CN取最大值,过点D作DQ⊥x轴,垂足为点Q,则△DQO∽△AOC,根据相似三角形的性质可设点D的坐标为(﹣3t,4t),利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之取其负值即可得出t值,再将其代入点D的坐标即可得出结论.
(1)∵直线y=![]() x+3与x轴、y轴分别交于A、C两点,
x+3与x轴、y轴分别交于A、C两点,
∴点A的坐标为(﹣4,0),点C的坐标为(0,3).
∵点B在x轴上,点B的横坐标为![]() ,
,
∴点B的坐标为(![]() ,0),
,0),
设抛物线的函数关系式为y=ax2+bx+c(a≠0),
将A(﹣4,0)、B(![]() ,0)、C(0,3)代入y=ax2+bx+c,得:
,0)、C(0,3)代入y=ax2+bx+c,得:
 ,解得:
,解得: ,
,
∴抛物线的函数关系式为y=﹣![]() x2﹣
x2﹣![]() x+3;
x+3;
(2)如图1,过点P作PE⊥x轴,垂足为点E,
∵△PCD、△PAD有相同的高,且S△PCD=2S△PAD,
∴CP=2AP,
∵PE⊥x轴,CO⊥x轴,
∴△APE∽△ACO,
∴![]() ,
,
∴AE=![]() AO=
AO=![]() ,PE=
,PE=![]() CO=1,
CO=1,
∴OE=OA﹣AE=![]() ,
,
∴点P的坐标为(﹣![]() ,1);
,1);
(3)如图2,连接AC交OD于点F,
∵AM⊥OD,CN⊥OD,
∴AF≥AM,CF≥CN,
∴当点M、N、F重合时,AM+CN取最大值,
过点D作DQ⊥x轴,垂足为点Q,则△DQO∽△AOC,
∴![]() ,
,
∴设点D的坐标为(﹣3t,4t).
∵点D在抛物线y=﹣![]() x2﹣
x2﹣![]() x+3上,
x+3上,
∴4t=﹣3t2+![]() t+3,
t+3,
解得:t1=﹣![]() (不合题意,舍去),t2=
(不合题意,舍去),t2=![]() ,
,
∴点D的坐标为(![]() ,
,![]() ),
),
故当AM+CN的值最大时,点D的坐标为(![]() ,
,![]() ).
).


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
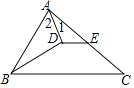
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的k个数:x1,x2,…,xk,称为数列Ak:x1,x2,…,xk,其中k为整数且k≥3.
定义V(Ak)=|x1﹣x2|+|x2﹣x3|+…+|xk﹣2﹣xk﹣1|+|xk﹣1﹣xk|.
例如,若数列A5:1,2,3,4,5,则V(A5)=|1﹣2|+|2﹣3|+|3﹣4|+|4﹣5|=4.
根据以上材料,回答下列问题:
(1)已知数列A3:3,5,﹣2,求V(A3).
(2)已知数列A4:x1,x2,x3,x4,其中x1,x2,x3,x4为4个互不相等的整数,且x1=3,x4=7,V(A4)=4,直接写出满足条件的数列A4.
(3)已知数列A5:x1,x2,x3,x4,x5中的5个数均为非负整数,且x1+x2+x3+x4+x5=25,请直接写出V(A5)的最大值和最小值及对应的数列.
查看答案和解析>>
科目:初中数学 来源: 题型:
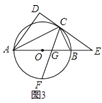
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
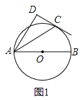
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
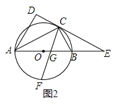
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,又过
,又过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 为
为![]() ,则下列说法:①
,则下列说法:①![]() 是
是![]() 的中点;②
的中点;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤连接
为等腰三角形;⑤连接![]() ,若
,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为24;其中正确的是______(填序号).
的面积为24;其中正确的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有库存1800套旧桌凳,修理后捐助贫困山区学校.现有甲,乙两个木工组都想承揽这项业务.经协商后得知:甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的![]() ,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
(1)求甲,乙两木工组单独修理这批桌凳的天数;
(2)现有三种修理方案供选择:方案一,由甲木工组单独修理这批桌凳;方案二,由乙木工组单独修理这批桌凳;方案三,由甲,乙两个木工组共同合作修理这批桌凳.请计算说明哪种方案学校付的修理费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是数学中最常见的定理之一,熟练的掌握勾股数,对迅速判断、解答题目有很大帮助,观察下列几组勾股数:
|
|
| |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
| |
… | … | … | … |
|
|
|
|
(1)你能找出它们的规律吗?(填在上面的横线上)
(2)你能发现![]() ,
,![]() ,
,![]() 之间的关系吗?
之间的关系吗?
(3)对于偶数,这个关系 (填“成立”或“不成立”)吗?
(4)你能用以上结论解决下题吗?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com