
����Ŀ����ͼ1����ֱ֪��![]() ��������
��������![]() ���ڵ�
���ڵ�![]() ��
��
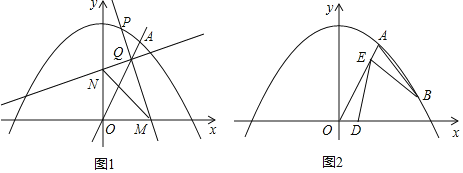
![]() ��ֱ��
��ֱ��![]() �Ľ���ʽ���߶�OA�ij��ȣ�
�Ľ���ʽ���߶�OA�ij��ȣ�
![]() ��PΪ�����ߵ�һ�����ڵĶ��㣬����P��ֱ��PM����x���������ڵ�
��PΪ�����ߵ�һ�����ڵĶ��㣬����P��ֱ��PM����x���������ڵ�![]() ��M��O���غ�
��M��O���غ�![]() ����ֱ��OA�ڵ�Q���ٹ���Q��ֱ��PM�Ĵ��ߣ���y���������ڵ�N������MN����
����ֱ��OA�ڵ�Q���ٹ���Q��ֱ��PM�Ĵ��ߣ���y���������ڵ�N������MN����![]() ������
������![]() ����Q�����ꣻ
����Q�����ꣻ
![]() ��ͼ2������BΪ�������϶Գ����Ҳ�ĵ㣬��E���߶�OA��
��ͼ2������BΪ�������϶Գ����Ҳ�ĵ㣬��E���߶�OA��![]() ���O��A���غ�
���O��A���غ�![]() ����
����![]() ��x���������ϵĶ��㣬������
��x���������ϵĶ��㣬������![]() ����̽����mȡ��ֵʱ������������E��ĸ���ֻ��1����
����̽����mȡ��ֵʱ������������E��ĸ���ֻ��1����
���𰸡���1��![]() ��2��2,
��2��2,![]() ��3����
��3����![]() ʱ��E��ֻ��1��
ʱ��E��ֻ��1��
��������
��1�����ô���ϵ�������ɽ�����⣻
��2����ͼ1�У�����Q��![]() ���ڵ�G��
���ڵ�G��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��QH��QM�غ�ʱ����ȻQG��QN�غϣ���ʱ
��QH��QM�غ�ʱ����ȻQG��QN�غϣ���ʱ![]() ��
��![]() ��QH��QM���غ�ʱ����
��QH��QM���غ�ʱ����![]() ��
��![]() �����ɽ�����⣻
�����ɽ�����⣻
��3�����ͼ2�У��ӳ�AB��x���ڵ�F������F��![]() �ڵ�C������A��
�ڵ�C������A��![]() ���ڵ�
���ڵ�![]() ���������F���꣬AB�ij�����֤��
���������F���꣬AB�ij�����֤��![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ���ɵ�
���ɵ�![]() ���Ƴ�
���Ƴ�![]() �����ö��κ��������ʽ�����⼴�ɣ�
�����ö��κ��������ʽ�����⼴�ɣ�
�⣺![]() �ѵ�
�ѵ�![]() ����
����![]() �ã�
�ã�
![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��ͼ1�У�����Q��
��ͼ1�У�����Q��![]() ���ڵ�G��
���ڵ�G��![]() ���ڵ�
���ڵ�![]() ��
��![]()
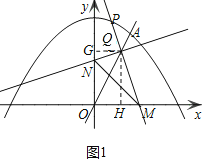
![]() ��QH��QM�غ�ʱ����ȻQG��QN�غϣ���ʱ
��QH��QM�غ�ʱ����ȻQG��QN�غϣ���ʱ![]() ��
��
![]() ��QH��QM���غ�ʱ��
��QH��QM���غ�ʱ��
![]() ��
��![]() ��
��
![]() ��
��
��![]()
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() span>��
span>��
![]() ��
��
���![]() ��
��
![]()
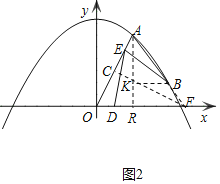
![]() ���ͼ2�У��ӳ�AB��x���ڵ�F������F��
���ͼ2�У��ӳ�AB��x���ڵ�F������F��![]() �ڵ�C������A��
�ڵ�C������A��![]() ���ڵ�R��
���ڵ�R��
![]() ��
��
![]() ��
��
![]()
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
���![]() ��
��
����B��![]() �ڵ�K����
�ڵ�K����![]() ��
��![]() ��
��
![]() ��
��
�� ��
��
���![]() ��
��![]() ��ȥ
��ȥ![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��ABҲ�ɲ�������ķ���
��ABҲ�ɲ�������ķ���![]()
��ֱ��AFΪ![]() �ѵ�
�ѵ�![]() ����
����![]() �����
�����
![]() ��
��![]() ��
��
![]() ��
��
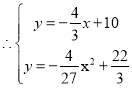 ��
��
![]() ��ȥ
��ȥ![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ����Ϊ
����Ϊ![]()
���ͼ3��

��![]() ʱ��
ʱ��![]() ����ʱE����1����
����ʱE����1����
��![]() ʱ����ȡһ��m��ֵ����Ӧ������aֵ����ʱE����2����
ʱ����ȡһ��m��ֵ����Ӧ������aֵ����ʱE����2����
![]() ��
��![]() ʱ��E��ֻ��1����
ʱ��E��ֻ��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������![]() ��ͼ����һ�κ���
��ͼ����һ�κ���![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() .
.
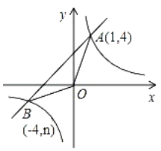
��1����һ�κ����ͷ����������Ľ���ʽ��
��2����![]() �������
�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֲ�������ڼ䣬С����С��������ͨ������ķ�ʽ������˭ȥ�μ�ѧУֲ������������£������������ڷֱ�װ���������1��2��3��4���ĸ��ͱ�������1��2��3��������ȫ��ͬ��С�ֱ�����������и�����һ������������������ϵ�����֮��С��5����ôС��ȥ���������С��ȥ��
��1������״ͼ���б������С��ȥ�ĸ��ʣ�
��2��С��˵�������ֹ���ƽ��������ͬ����˵������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����¡�̳�������Ϊ8Ԫ��ijС��Ʒ��ÿ��10Ԫ���ۣ�ÿ������۳�140������С��Ʒÿ����1Ԫ���������ͻ����10��.���̳��ڽ�������С������£���С��Ʒÿ�����ۼ�ӦΪ����Ԫʱ��ÿ�������Ϊ600Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F���ı���ABCD�ĶԽ���AC�ϵ����㣬AF=CE��DF=BE��DF��BE��

��֤����1����AFD�ա�CEB����2���ı���ABCD��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ͺ�����Դ���綯���������������ʣ�����![]() ��ǧ��ʱ����������ʻ·��
��ǧ��ʱ����������ʻ·��![]() ��ǧ�ף��ĺ���ͼ��.����˵��������ǣ� ��
��ǧ�ף��ĺ���ͼ��.����˵��������ǣ� ��
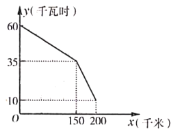
A.�����������س�����ʱ��������60ǧ��ʱ
B.����ʣ�����Ϊ35ǧ��ʱ����������ʻ��150ǧ��
C.����������ʻ180ǧ��ʱ�����ص�ʣ�����Ϊ20ǧ��ʱ
D.25ǧ��ʱ�ĵ�������������ʹ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ�뾶��ͬ��СԲ����ͼ��ʾ�Ĺ��ɰڷţ���1��ͼ����6��СԲ����2��ͼ����10��СԲ����3��ͼ����16��СԲ����4��ͼ����24��СԲ���������ι��ɣ���6��ͼ���У���������СԲ��

A.34B.40C.46D.60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
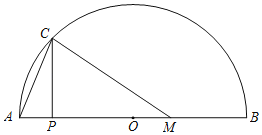
����Ŀ����ͼ���ڰ�Բ��AB�У�ֱ��AB��6cm����M��AB��һ�㣬MB��2cm��PΪAB��һ���㣬PC��AB��AB�ڵ�C������AC��CM����A��P�����ľ���Ϊxcm��A��C�����ľ���Ϊy1cm��C��M�����ľ���Ϊy2cm��
С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��

��3����Ϻ���ͼ������⣺
����AC��CMʱ���߶�AP��ȡֵ��Χ���� ����
������AMC�ǵ���������ʱ���߶�AP�ij�ԼΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�a��1��x2+2x+a��1=0��
��1�����÷�����һ��Ϊ2����a��ֵ�����̵���һ����
��2����aΪ��ֵʱ�����̽���һ�����������ʱa��ֵ�����̵ĸ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com