
��ͼ��ʾ����ֱ������ABCD�У�ABΪ��ֱ�ڵױߵ�����AD=1��BC=2��AB=3����EΪCD������C��D��һ�����㣬����E��AB�Ĵ��ߣ�����ΪF����ADE����AEB����BCE������ֱ�ΪS1��S2��S3��

��1����AF=x������x��ʾS1��S3�ij˻�S1S3������S1S3�����ֵ��
��2���� =t������t��ʾEF�ij���
=t������t��ʾEF�ij���
��3���ڣ�2���������£���tΪ��ֵʱ��S22=4S1S3��
�⣺��1����S1= AD•AF=
AD•AF= x��S3=
x��S3= BC•BF=
BC•BF= ��2����3��x��=3��x��
��2����3��x��=3��x��
��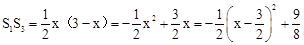 ��0��x��3����
��0��x��3����
�൱x=  ʱ��S1S3�����ֵΪ
ʱ��S1S3�����ֵΪ ��
��
��2����ͼ����DM��BC������ΪM��DM��EF�����N��

�� =t����AF=tFB��
=t����AF=tFB��
�ߡ�DNE�ס�DMC ��BM=MC=AD=1��
�� ����NE=
����NE= ��
��
��EF=FN+NE=1+ ��
��
��3����AB=AF+FB=��t+1��FB=3����FB= ����AF=tFB=
����AF=tFB= ��
��
��S1= AD•AF=
AD•AF= ��
�� =
= ��S3=
��S3= BC•FB=
BC•FB= ��2��
��2�� =
= ��
��
S2= AB•FE=
AB•FE= ��3��
��3�� =
= ��
��
��S1S3= ��S22=
��S22= ��
��
�� =4��
=4�� ����4t2��4t+1=0�����t=
����4t2��4t+1=0�����t= ��
��
�൱t= ʱ��S22=4S1S3��
ʱ��S22=4S1S3��
��������
�����������1��ֱ�Ӹ��������ε������ʽ��ɡ�
��2����DM��BC������ΪM��DM��EF�����N������ =t����֪AF=tFB�����ɡ�DNE�ס�DMC ��BM=MC=AD=1�ɵó�
=t����֪AF=tFB�����ɡ�DNE�ס�DMC ��BM=MC=AD=1�ɵó� ������NE=
������NE= ������EF=FN+NE���ɵó����ۡ�
������EF=FN+NE���ɵó����ۡ�
��3������AB=AF+FB=��t+1��FB=3���ɵó�FB= ���ʿɵó�AF=tFB=
���ʿɵó�AF=tFB= �����������ε������ʽ����t��ʾ��S1��S3��S2����s22=4S1S3�����ɵó�t��ֵ��
�����������ε������ʽ����t��ʾ��S1��S3��S2����s22=4S1S3�����ɵó�t��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 27����ͼ��ʾ����ֱ������ABCD�У�AD��BC��AD=24cm��AB=8cm��BC=26cm������P��A�㿪ʼ��AD����D��1cm/s���ٶ��˶�������Q��C�㿪ʼ��CB����B��3cm/s���ٶ��˶���P��Q�ֱ��A��Cͬʱ������������һ�㵽�˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��s����t�ֱ�Ϊ��ֵʱ���ı���PQCD��ƽ���ı��Σ��������Σ�
27����ͼ��ʾ����ֱ������ABCD�У�AD��BC��AD=24cm��AB=8cm��BC=26cm������P��A�㿪ʼ��AD����D��1cm/s���ٶ��˶�������Q��C�㿪ʼ��CB����B��3cm/s���ٶ��˶���P��Q�ֱ��A��Cͬʱ������������һ�㵽�˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��s����t�ֱ�Ϊ��ֵʱ���ı���PQCD��ƽ���ı��Σ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
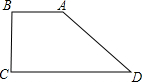 ��ͼ��ʾ����ֱ������ABCD�У�AB��CD����B=��C=90�㣬AD=20��BC=10�����A�͡�D�ֱ��ǣ�������
��ͼ��ʾ����ֱ������ABCD�У�AB��CD����B=��C=90�㣬AD=20��BC=10�����A�͡�D�ֱ��ǣ�������| A��30�㣬150�� | B��45�㣬135�� | C��120�㣬60�� | D��150�㣬30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
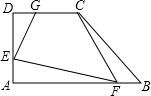 ��ͼ��ʾ����ֱ������ABCD�У���A=��D=90�㣬��ȡAE=BF=DG=x����֪AB=6��CD=3��AD=4�����ı���CGEF�����S����x�ĺ�������ʽ��x��ȡֵ��Χ��
��ͼ��ʾ����ֱ������ABCD�У���A=��D=90�㣬��ȡAE=BF=DG=x����֪AB=6��CD=3��AD=4�����ı���CGEF�����S����x�ĺ�������ʽ��x��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
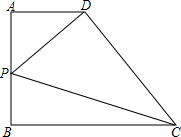 ��ͼ��ʾ����ֱ������ABCD�У�AB=2��P�DZ�AB���е㣬��PDC=90�㣬������ABCD�������Сֵ�Ƕ��٣�
��ͼ��ʾ����ֱ������ABCD�У�AB=2��P�DZ�AB���е㣬��PDC=90�㣬������ABCD�������Сֵ�Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•ɽ��ģ�⣩��ͼ��ʾ����ֱ������ABCD�У�AB��CD����EΪAB���е㣬��FΪBC���е㣬AB=4��EF=2����B=60�㣬��AD�ij�Ϊ
��2013•ɽ��ģ�⣩��ͼ��ʾ����ֱ������ABCD�У�AB��CD����EΪAB���е㣬��FΪBC���е㣬AB=4��EF=2����B=60�㣬��AD�ij�Ϊ| 3 |
| 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com