Question

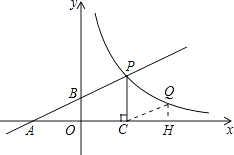
【题目】如图，直线y=ax+1与x轴、y轴分别相交于A、B两点，与双曲线y= （x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（﹣2，0）．

（1）求双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．

Answer 1

【答案】
（1）

解：把A（﹣2，0）代入y=ax+1中，求得a= ，

∴y= x+1，

由PC=2，把y=2代入y= x+1中，得x=2，即P（2，2），

把P代入y= 得：k=4，

则双曲线解析式为y= ；

（2）

解：设Q（a，b），

∵Q（a，b）在y= 上，

∴b= ，

当△QCH∽△BAO时，可得 = ，即 = ，

∴a﹣2=2b，即a﹣2= ，

解得：a=4或a=﹣2（舍去），

∴Q（4，1）；

当△QCH∽△ABO时，可得 = ，即 = ，

整理得：2a﹣4= ，

解得：a=1+ 或a=1﹣ （舍），

∴Q（1+ ，2 ﹣2）．

综上，Q（4，1）或Q（1+ ，2 ﹣2）．

【解析】（1）把A坐标代入直线解析式求出a的值，确定出直线解析式，把y=2代入直线解析式求出x的值，确定出P坐标，代入反比例解析式求出k的值，即可确定出双曲线解析式；（2）设Q（a，b），代入反比例解析式得到b= ，分两种情况考虑：当△QCH∽△BAO时；当△QCH∽△ABO时，由相似得比例求出a的值，进而确定出b的值，即可得出Q坐标．