
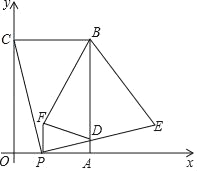
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
【答案】(1)、(t+6,t);(2)、当t=2时,S有最小值是16;(3)、理由见解析.
【解析】分析:(1)、过点E作EG⊥x轴于点G,根据题意得出CO=AB=6、OA=BC=4、OP=t,然后通过角之间的关系证明△PCO和△EPG全等,从而得出答案;(2)、根据DA∥EG得出△PAD和△PGE相似,求出AD的长度,然后根据四边形的面积等于△BDF的面积加上△BDE的面积得出函数解析式,从而求出面积的最值;(3)、根据∠FBD、∠FDB、∠BFD分别为直角,证明是否存在即可得出答案.
详解:(1)如图所示,过点E作EG⊥x轴于点G,则∠COP=∠PGE=90°,
由题意知CO=AB=6、OA=BC=4、OP=t,∵PE⊥CP、PF⊥OP,
∴∠CPE=∠FPG=90°,即∠CPF+∠FPE=∠FPE+∠EPG,∴∠CPF=∠EPG,
又∵CO⊥OG、FP⊥OG,∴CO∥FP,∴∠CPF=∠PCO,∴∠PCO=∠EPG,
在△PCO和△EPG中,∵∠PCO=∠EPG,∠POC=∠EGP,PC=EP,∴△PCO≌△EPG(AAS),
∴CO=PG=6、OP=EG=t,则OG=OP+PG=6+t,则点E的坐标为(t+6,t),
(2)∵DA∥EG,∴△PAD∽△PGE,∴![]() ,∴
,∴![]() ,∴AD=
,∴AD=![]() t(4﹣t),
t(4﹣t),
∴BD=AB﹣AD=6﹣![]() t(4﹣t)=
t(4﹣t)=![]() t2﹣
t2﹣![]() t+6,∵EG⊥x轴、FP⊥x轴,且EG=FP,
t+6,∵EG⊥x轴、FP⊥x轴,且EG=FP,
∴四边形EGPF为矩形,∴EF⊥BD,EF=PG,
∴S四边形BEDF=S△BDF+S△BDE=![]() ×BD×EF=
×BD×EF=![]() ×(
×(![]() t2﹣
t2﹣![]() t+6)×6=
t+6)×6=![]() (t﹣2)2+16,
(t﹣2)2+16,
∴当t=2时,S有最小值是16;
(3)①假设∠FBD为直角,则点F在直线BC上∵PF=OP<AB,
∴点F不可能在BC上,即∠FBD不可能为直角;
②假设∠FDB为直角,则点F在EF上,∵点D在矩形的对角线PE上,
∴点D不可能在EF上,即∠FDB不可能为直角;
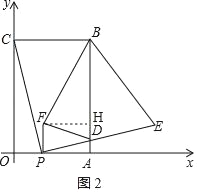
③假设∠BFD为直角且FB=FD,则∠FBD=∠FDB=45°如图2,作FH⊥BD于点H,
则FH=PA,即4﹣t=6﹣t,方程无解,
∴假设不成立,即△BDF不可能是等腰直角三角形.



科目:初中数学 来源: 题型:
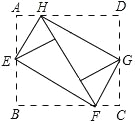
【题目】如图所示,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于( )
A. 25:24 B. 16:15 C. 5:4 D. 4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() 的解析式为
的解析式为![]() ,直线
,直线 ![]() 的解析式为
的解析式为![]() ,
,![]() 为
为![]() 上的一点,且
上的一点,且![]() 点的坐标为
点的坐标为![]() 作直线
作直线 ![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]() 于点
于点![]() ,交直线
,交直线 ![]() 于点
于点![]() ,作
,作![]() 轴,交直线于
轴,交直线于![]() 点
点![]() ,再作
,再作![]()
![]() 于点
于点![]() ,作
,作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ....按此作法继续作下去,则
....按此作法继续作下去,则 ![]() 的坐标为_____,
的坐标为_____,![]() 的坐标为______
的坐标为______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
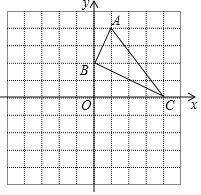
【题目】如图,已知网格上最小的正方形的边长为![]() (长度单位),点
(长度单位),点![]() 在格点上.
在格点上.
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点
(点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() );
);
(2)![]() 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);
(3)点![]() 到直线
到直线![]() 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空);
查看答案和解析>>
科目:初中数学 来源: 题型:
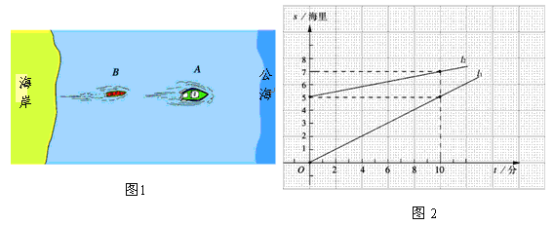
【题目】我国边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防部迅速派出快艇
正向公海方向行驶,边防部迅速派出快艇![]() 追赶(如图1) .图2中
追赶(如图1) .图2中![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.根据图象问答问题:
(分)之间的关系.根据图象问答问题:
(1)①直线![]() 与直线
与直线![]() 中 表示
中 表示![]() 到海岸的距离与追赶时间之间的关系;
到海岸的距离与追赶时间之间的关系;
②![]() 与
与![]() 比较 速度快;
比较 速度快;
③如果一直追下去,那么![]() ________ (填 “能”或“不能")追上
________ (填 “能”或“不能")追上![]() ;
;
④可疑船只![]() 速度是 海里/分,快艇
速度是 海里/分,快艇![]() 的速度是 海里/分;
的速度是 海里/分;
(2)![]() 与
与![]() 对应的两个一次函数表达式
对应的两个一次函数表达式![]() 与
与![]() 中
中![]() 的实际意义各是什么?并直接写出两个具体表达式.
的实际意义各是什么?并直接写出两个具体表达式.
(3)![]() 分钟内
分钟内![]() 能否追上
能否追上![]() ?为什么?
?为什么?
(4)当![]() 逃离海岸
逃离海岸![]() 海里的公海时,
海里的公海时, 将无法对其进行检查,照此速度,
将无法对其进行检查,照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?为什么?
逃入公海前将其拦截?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
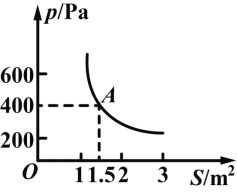
【题目】某科技小组进行野外考察,途中遇到一片十几米宽的泥地,他们沿着前进路线铺了若干块木板,构成一条临时近道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
(1)写出这一函数的关系式和自变量的取值范围.
(2)当木板面积为0.2m2时,压强是多少?
(3)如果要求压强不超过6000Pa,那么木板的面积至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 与边
与边![]() 的垂直平分线
的垂直平分线![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,现有下列结论:①
,现有下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )

A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com