
【题目】如图,正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上一个动点,连结
上一个动点,连结![]() ,过
,过![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分别为垂足.
分别为垂足.
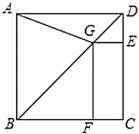
(1)求证:![]() ;
;
(2)①写出![]() 、
、![]() 、
、![]() 三条线段满足的等量关系,并证明;②求当
三条线段满足的等量关系,并证明;②求当![]() ,
,![]() 时,
时,![]() 的长
的长
【答案】(1)见解析;(2)①GE2+GF2=AG2,证明见解析;②![]() 的长为
的长为![]() 或
或![]() .
.
【解析】
(1)根据正方形的性质得出△DGE和△BGF是等腰直角三角形,可得GE=![]() DG,GF=
DG,GF=![]() BG,结合AB=
BG,结合AB=![]() BD即可得出结论;
BD即可得出结论;
(2)①连接CG,由SAS证明△ABG≌△CBG,得出AG=CG,证出四边形EGFC是矩形,得出CE=GF,由勾股定理即可得出GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,由①中结论得出方程求出CF=1或CF=5,再分情况讨论,由勾股定理求出BG即可.
解:(1)∵四边形ABCD为正方形,
∴∠BCD=90°,∠ABD=∠CDB=∠CBD=45°,AB=BC=CD,
∴△ABD是等腰直角三角形,
∴AB=![]() BD,
BD,
∵GE⊥CD,GF⊥BC,
∴△DGE和△BGF是等腰直角三角形,
∴GE=![]() DG,GF=
DG,GF=![]() BG,
BG,
∴GE+GF=![]() (DG+BG)=
(DG+BG)=![]() BD,
BD,
∴GE+GF=AB;
(2)①GE2+GF2=AG2,
证明:连接CG,如图所示:

在△ABG和△CBG中,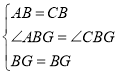 ,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,
∵GE⊥CD,GF⊥BC,∠BCD=90°,
∴四边形EGFC是矩形,
∴CE=GF,
∵GE2+CE2=CG2,
∴GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,
∵GE2+GF2=AG2,
∴![]() ,
,
解得:x=1或x=5,
当x=1时,则BF=GF=5,
∴BG=![]() ,
,
当x=5时,则BF=GF=1,
∴BG=![]() ,
,
综上,![]() 的长为
的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
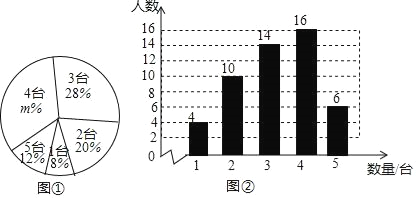
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
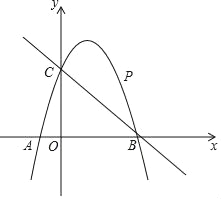
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
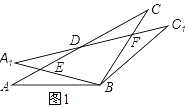
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
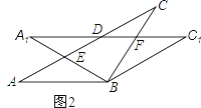
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
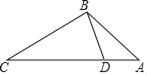
A. ∠ABD=∠C B. ∠ADB=∠ABC C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
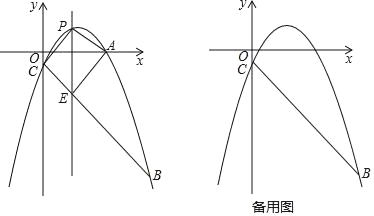
【题目】如图,已知抛物线y=﹣![]() x2+bx+c经过点A(5,
x2+bx+c经过点A(5,![]() )、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
(1)求抛物线对应的函数解析式;
(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;
(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.
①求点P和点F的坐标;
②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
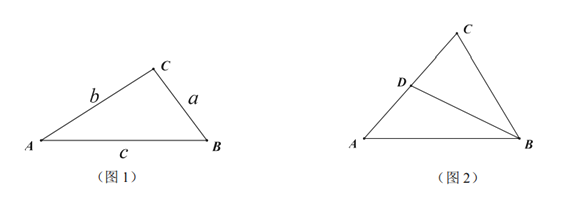
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com